��Ŀ����
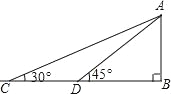
����Ŀ���ڵ���ֱ��������ABC�У���C=90�㣬AC=BC=10cm������ֱ��������DEF�Ķ���DΪAB���е㣮
��1����ͼ��1����ʾ��DE��AC��M��BC��DF��N����DM��DN����������ʲô��ϵ�������������ص����ֵ�����Ƕ��٣�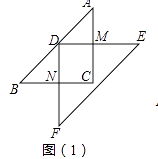
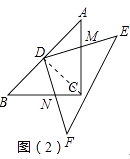
��2���ڣ�1���Ļ����ϣ���������DEF���ŵ�D��תһ���ĽǶȣ���AC��DE�ཻ��M��BC��DF�ཻ��N����ͼ��2������DM��DN����������ʲô��ϵ�������������ص����ֵ�����Ƕ��٣�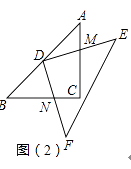
���𰸡�
��1��
�⣺����DC��
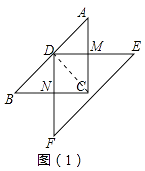
��AC=BC��DΪAB���е㣬��ACB=90�㣬
��CD��AB����ACD=��BCD=45�㣬��A=��B=45�㣬
���A=��DCN��AD=DC��
��DM��AC��DN��BC��
���DMA=��DNC��
���ADM�ա�CDN��AAS����
��DM=DN��
��S�ص�=S��DNC+S��DMC=S��DMA+S��DMC=S��ADC= ![]() S��ABC=
S��ABC= ![]() ��
�� ![]() ��1��1=
��1��1= ![]() ��cm2��
��cm2��
��2��
�⣺����CD����CD��AB����A=��DCB=45�㣬AD=CD��
�ߡ�ADM+��MDC=��MDC+��CDF=90�㣬
���ADM=��CDN��
���AMD�ա�CND��ASA����
��DM=DN��
ͬ��1���ɵ�S�ص�= ![]() S��ABC=
S��ABC= ![]() ��
�� ![]() ��1��1=
��1��1= ![]() ��cm2��
��cm2��
����������1������DC���ɵ���ֱ��������ABC��DΪAB�е㣬�������ߺ�һ�õ�CD��ֱ��AB�������Խ���ȣ�����AAS�õ�������ADM��������CDNȫ�ȣ�����ȫ�������ζ�Ӧ����ȵõ�DM=DN���ص������������������DNC��������DMC���֮�ͣ�������������������ADC�������Ϊ������ABC���һ�룬������ɣ���2������DC���ɵ���ֱ��������ABC��DΪAB�е㣬�������ߺ�һ�õ�CD��AB����A=��DCB=45�㣬AD=CD������ͬ�ǵ������ȵõ���ADM=��CDN������ASA�õ����Ǽ�AMD��������CDNȫ�ȣ�����ȫ�������ζ�Ӧ����ȵõ�DM=DN��ͬ��1������ص�����������ɣ�