ЬтФПФкШн
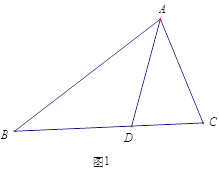
ЁОЬтФПЁПвбжЊЃКШчЭМЫљЪОЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЌBC=5cmЃЌAC=7cm. СНИіЖЏЕуPЁЂQЗжБ№ДгBЁЂCСНЕуЭЌЪБГіЗЂЃЌЦфжаЕуPвд1РхУз/УыЕФЫйЖШбизХЯпЖЮBCЯђЕуCдЫЖЏЃЌЕуQвд2РхУз/УыЕФЫйЖШбизХЯпЖЮCAЯђЕуAдЫЖЏ.
ЃЈ1ЃЉPЁЂQСНЕудкдЫЖЏЙ§ГЬжаЃЌОЙ§МИУыКѓЃЌЁїPCQЕФУцЛ§ЕШгк4РхУз2ЃПОЙ§МИУыКѓPQЕФГЄЖШЕШгк5РхУзЃП
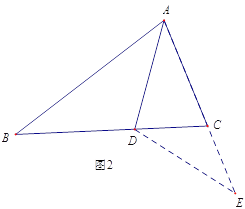
ЃЈ2ЃЉдкPЁЂQСНЕудкдЫЖЏЙ§ГЬжаЃЌЫФБпаЮABPQЕФУцЛ§ФмЗёЕШгк11РхУз2ЃПЪдЫЕУїРэгЩ.

ЁОД№АИЁПЃЈ1ЃЉОЙ§1УыКѓЃЌЁїPCQЕФУцЛ§ЕШгк4РхУз2ЃЛОЙ§2УыКѓPQЕФГЄЖШЕШгк5РхУзЃЛЃЈ2ЃЉЫФБпаЮABPQЕФУцЛ§ВЛПЩФмЕШгк11РхУз2.
ЁОНтЮіЁП
ЃЈ1ЃЉШєЪЙЦфУцЛ§ЮЊ4ЃЌМДSЁїPCQ= PCQC=4ЃЌДњШыЪ§ОнЧѓНтМДПЩЃЛИљОнЙДЙЩЖЈРэПЩЕУЗНГЬ,МДПЩЧѓГіtЕФжЕ;
PCQC=4ЃЌДњШыЪ§ОнЧѓНтМДПЩЃЛИљОнЙДЙЩЖЈРэПЩЕУЗНГЬ,МДПЩЧѓГіtЕФжЕ;
ЃЈ2ЃЉШєЫФБпаЮABPQЕФУцЛ§ФмЗёЕШгк11ЃЌМДSЁїPCQ= -11=
-11= ЃЌНЈСЂЗНГЬЃЌНтЗНГЬПДЪЧЗёгаНтЃЌШєгаЃЌдђДцдк.
ЃЌНЈСЂЗНГЬЃЌНтЗНГЬПДЪЧЗёгаНтЃЌШєгаЃЌдђДцдк.
ЃЈ1ЃЉЃЈiЃЉЩшОЙ§xУыКѓЃЌЁїPCQЕФУцЛ§ЕШгк4РхУз2ЃЌДЫЪБЃЌPC=5-xЃЌCQ=2x.
гЩЬтвтЃЌЕУ  ЃЌећРэЃЌЕУx2-5x+4=0. НтЕУx1=1ЃЌx2=4.
ЃЌећРэЃЌЕУx2-5x+4=0. НтЕУx1=1ЃЌx2=4.
ЕБx=4ЪБЃЌ2x=8ЃО7ЃЌДЫЪБЕуQдНЙ§AЕуЃЌВЛКЯЬтвтЃЌЩсШЅ.
МДОЙ§1УыКѓЃЌЁїPCQЕФУцЛ§ЕШгк4РхУз2.
ЃЈiiЃЉЩшОЙ§tУыКѓPQЕФГЄЖШЕШгк5РхУз. гЩЙДЙЩЖЈРэЃЌЕУ(5-t)2+(2t)2=52 .
ећРэЃЌЕУt2-2t=0. НтЕУt1=2ЃЌt2=0(ВЛКЯЬтвтЃЌЩсШЅ).
Д№ЃКОЙ§2УыКѓPQЕФГЄЖШЕШгк5РхУз.
ЃЈ2ЃЉЩшОЙ§mУыКѓЃЌЫФБпаЮABPQЕФУцЛ§ЕШгк11РхУз2.гЩЬтвтЃЌЕУ .ећРэЃЌЕУm2-5m+6.5=0.
.ећРэЃЌЕУm2-5m+6.5=0.
ЁпЁї=(-5)2-4ЁС6.5=-1ЃМ0ЃЌ ЁрЗНГЬУЛгаЪЕЪ§Иљ.
МДЫФБпаЮABPQЕФУцЛ§ВЛПЩФмЕШгк11РхУз2.

 ССЕуМЄЛюОЋБрЬсгХ100ЗжДѓЪдОэЯЕСаД№АИ
ССЕуМЄЛюОЋБрЬсгХ100ЗжДѓЪдОэЯЕСаД№АИ