题目内容
从社会效益和经济效益出发,某地制定了三年规划,投入资金进行生态环境建设,并以此发展旅游产业.根据规划,第一年度投入资金800万元,第二年度比第一年度减少| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 13 |
分析:本题考查一元二次方程的应用,解决此类两次变化问题,可利用公式a(1+x)2=c,其中a是变化前的原始量,c是两次变化后的量,x表示平均每次的增长率,由此列出方程即可求出结果.
解答:解:设三年内旅游业收入每年的平均增长率为x,
根据题意得方程:
400+400(1+x)+400(1+x)2=800+800×(1-
)+800×(1-
)×(1-
),
化简得x2+3x-1=0,
解得x1=
,x2=
(不合题意,应舍去),
∴x=
≈
=0.303≈30%.
答:三年内旅游业收入每年的平均增长率应约30%.
根据题意得方程:
400+400(1+x)+400(1+x)2=800+800×(1-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
化简得x2+3x-1=0,
解得x1=
-3+
| ||
| 2 |
-3-
| ||
| 2 |
∴x=
| ||
| 2 |
| 3.606-3 |
| 2 |
答:三年内旅游业收入每年的平均增长率应约30%.
点评:本题的关键语为:三年内的投入资金与旅游业总收入持平.根据关键语找到等量关系是解决本题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
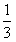 ,第三年度比第二年度减少
,第三年度比第二年度减少 ,第一年度当地旅游业收入估计为400万元,要使三年内的投入资金与旅游业总收入持平,则旅游业收入的年平均增长率应是多少?(以下数据供选用:
,第一年度当地旅游业收入估计为400万元,要使三年内的投入资金与旅游业总收入持平,则旅游业收入的年平均增长率应是多少?(以下数据供选用: ,计算结果精确到百分位)
,计算结果精确到百分位) ,第三年度比第二年度减少
,第三年度比第二年度减少 .第一年度当地旅游业收入估计为400万元,要使三年内的投入资金与旅游业总收入持平,则旅游业收入的年平均增长率应是多少?(以下数据供选用:
.第一年度当地旅游业收入估计为400万元,要使三年内的投入资金与旅游业总收入持平,则旅游业收入的年平均增长率应是多少?(以下数据供选用: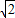 ≈1.414,
≈1.414, ≈3.606,计算结果精确到百分位)
≈3.606,计算结果精确到百分位)