Question

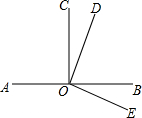如图，CO⊥AB于点O，OD⊥OE，则图中相等的角有

1. A.
   3对
2. B.
   4对
3. C.
   5对
4. D.
   6对

Answer 1

C
分析：根据直角都相等找出相等的对数，再根据等角的余角相等求出∠BOE=∠COD，然后都加上一个直角可得∠AOD=∠COE，从而最后得解．
解答：∵CO⊥AB于点O，OD⊥OE，
∴∠AOC=∠BOC=∠DOE=90°，
∴∠AOC=∠BOC，∠AOC=∠DOE，∠BOC=∠DOE，共3对，
∵∠BOD+∠BOE=90°，∠BOD+∠COD=90°，
∴∠BOE=∠COD，
又∵∠AOD=∠COD+90°，∠COE=∠BOE+90°，
∴∠AOD=∠COE，
综上所述，共有3+1+1=5对．
故选C．
点评：本题考查了余角与补角，熟记概念并准确识图是解题的关键，要注意三个直角可以组成3对相等的角．