题目内容
已知等腰三角形有一个角是40°，那么它腰上的高线和底边的夹角是（ ）
| A、20° | B、50° | C、20°或50° | D、大小无法确定 |
分析：分40°的角是顶角或底角两种情况进行讨论，即可求解．
解答：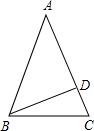
解：当40°的角是顶角时：
∴∠ACB=
=70°
在直角△BCD中，∠CBD=90°-70°=20°；
当40°的角是底角时，
即∠ACB=40°，
在直角△BCD中，∠CBD=90°-∠ACB=50°，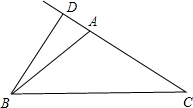
故腰上的高线和底边的夹角是20°或50°．
故选C．
解：当40°的角是顶角时：∴∠ACB=
| 180-40 |
| 2 |
在直角△BCD中，∠CBD=90°-70°=20°；
当40°的角是底角时，
即∠ACB=40°，
在直角△BCD中，∠CBD=90°-∠ACB=50°，
故腰上的高线和底边的夹角是20°或50°．
故选C．
点评：本题主要考查了等腰三角形的角度的计算，正确作出图形，分两种情况讨论是解题关键．
练习册系列答案
相关题目