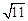题目内容
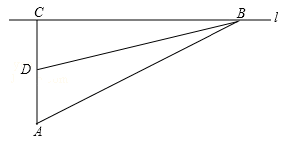
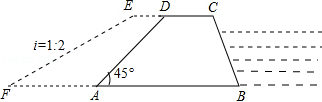
如图,马路的两边CF、DE互相平行,线段CD为人行横道,马路两侧的A、B两点分别表示车站和超市。CD与AB所在直线互相平行,且都与马路两边垂直,马路宽20米,A,B相距62米,
∠A=67°,∠B=37°

(1)求CD与AB之间的距离;
(2)某人从车站A出发,沿折线A→D→C→B去超市B,求他沿折线A→D→C→B到达超市比直接横穿马路多走多少米
(参考数据: )
)
∠A=67°,∠B=37°

(1)求CD与AB之间的距离;
(2)某人从车站A出发,沿折线A→D→C→B去超市B,求他沿折线A→D→C→B到达超市比直接横穿马路多走多少米
(参考数据:
 )
)解:(1)设CD与AB之间的距离为x米,即CF=DE=x米,
在Rt△BCF和Rt△ADE中,∵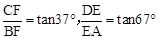 ,
,
∴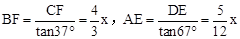 。
。
又∵AB=62,CD=20,∴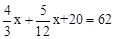 ,解得:x=24。
,解得:x=24。
∴CD与AB之间的距离为24米。
(2)在Rt△BCF和Rt△ADE中,
∵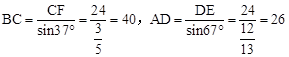 ,
,
∴AD+DC+CB-AB=40+20+26-62=24(米).
答:他沿折线A→D→C→B到达超市比直接横穿马路多走24米
在Rt△BCF和Rt△ADE中,∵
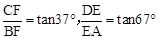 ,
,∴
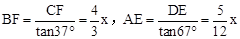 。
。又∵AB=62,CD=20,∴
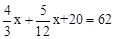 ,解得:x=24。
,解得:x=24。∴CD与AB之间的距离为24米。
(2)在Rt△BCF和Rt△ADE中,
∵
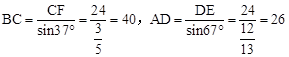 ,
,∴AD+DC+CB-AB=40+20+26-62=24(米).
答:他沿折线A→D→C→B到达超市比直接横穿马路多走24米
试题分析:(1)设CD与AB之间的距离为x,则在Rt△BCF和Rt△ADE中分别用x表示BF,AE,又AB=AE+EF+FB,代入即可求得x的值。
(2)在Rt△BCF和Rt△ADE中,分别求出BC、AD的长度,求出AD+DC+CB-AB的值即可求解。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
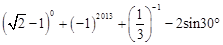
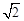
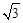
 ,
,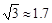 ,结果保留整数.)
,结果保留整数.)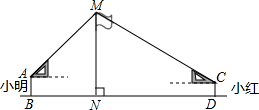
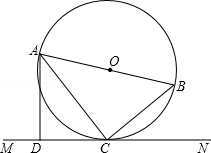
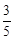 ,求⊙O的半径.
,求⊙O的半径.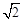 =1.41,
=1.41,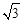 =1.73)
=1.73)