题目内容
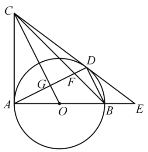
【题目】如图,已知AB为⊙O的直径,AC为⊙O的切线,连结CO,过B作BD∥OC交⊙O于D,连结AD交OC于G.延长AB、CD交于点E.
(1)求证:CD是⊙O的切线;
(2)若BE=2,DE=4,求CD的长;
(3)在(2)的条件下,连结BC交AD于F,求![]() 的值.
的值.
【答案】(1)见解析;(2)6;(3)![]() .
.
【解析】
(1)连接OD,由切线的性质和圆周角定理可得∠CAB=90°=∠ADB,由“SAS”判定△CDO≌△CAO,则∠CDO=∠CAO=90°,然后根据切线的判定定理可得到CD是⊙O的切线;
(2)设⊙O半径为r,则OD=OB=r,在Rt△ODE中利用勾股定理得到r2+42=(r+2)2,解得r=3,即OB=3,然后根据平行线分线段成比例定理,由DB∥OC得到DE:CD=BE:OB,于是可计算出CD=6;
(3)由△CDO≌△CAO得到AC=CD=6,在Rt△AOC中利用勾股定理计算出OC=3![]() ,再证明Rt△OAG∽△OCA,利用相似比计算出OG=
,再证明Rt△OAG∽△OCA,利用相似比计算出OG=![]() ,则CG=OC-OG=
,则CG=OC-OG=![]() ,易得BD=2OG=
,易得BD=2OG=![]() ,然后利用CG∥BD得到
,然后利用CG∥BD得到![]() .
.
证明:(1)如图,连接OD,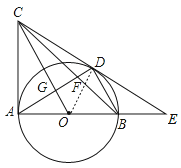
∵AC为⊙O的切线,AB为⊙O的直径,
∴∠CAB=90°=∠ADB,
∵OD=OB,
∴∠DBO=∠BDO,
∵CO∥BD,
∴∠AOC=∠OBD,∠COD=∠ODB,
∴∠AOC=∠COD,且AO=OD,CO=CO,
∴△AOC≌△DOC(SAS)
∴∠CAO=∠CDO=90°,
∴OD⊥CD,且OD是半径,
∴CD是⊙O的切线;
(2)设⊙O半径为r,则OD=OB=r,
在Rt△ODE中,∵OD2+DE2=OE2,
∴r2+42=(r+2)2,解得r=3,
∴OB=3,
∵DB∥OC,
∴![]()
即![]()
∴CD=6;
(3)由(1)得△CDO≌△CAO,
∴AC=CD=6,
在Rt△AOC中,OC=![]() ,
,
∵∠AOG=∠COA,
∴△OAG∽△OCA,
∴![]() ,
,
即![]() ,
,
∴OG=![]() ,
,
∴CG=OC-OG=3![]() -
-![]() =
=![]() ,
,
∵OG∥BD,OA=OB,
∴OG为△ABD的中位线,
∴BD=2OG=![]() ,
,
∵CG∥BD,
∴![]()
∴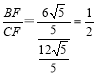 .
.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案【题目】如图,A,B,C为⊙O上的定点.连接AB,AC,M为AB上的一个动点,连接CM,将射线MC绕点M顺时针旋转90°,交⊙O于点D,连接BD.若AB=6cm,AC=2cm,记A,M两点间距离为xcm,B,D两点间的距离为ycm.
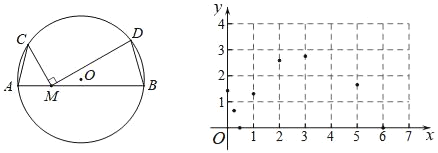
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东探究的过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表,补全表格:
x/cm | 0 | 0.25 | 0.47 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 1.43 | 0.66 | 0 | 1.31 | 2.59 | 2.76 |
| 1.66 | 0 |
(2)在平面直角坐标系xOy中,描出补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当BD=AC时,AM的长度约为 cm.