题目内容
7、如图所示，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置，若∠EFB=65°，则∠AED′等于（ ）分析：已知∠EFB=65°，欲求∠AED′，可通过折叠的性质，结合三角形内角和定理求解．
解答：解：根据折叠的性质，折叠前后角相等，
即∠DEF=∠FED′，
又根据AD∥BC，得∠DEF=∠EFB，
因此∠DEF=∠FED'=65°，
则∠AED′=180°-65°-65°=50°．
故选C．
即∠DEF=∠FED′，
又根据AD∥BC，得∠DEF=∠EFB，
因此∠DEF=∠FED'=65°，
则∠AED′=180°-65°-65°=50°．
故选C．
点评：本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
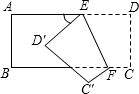（2010•龙岩模拟）如图所示，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置．若∠EFB=70°，则∠AED′等于（ ）
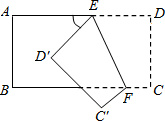如图所示，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置．若∠AED′=65°，则∠BFC′等于
