题目内容
f(x)表示关于x的函数,若x1,x2在x的取值范围内,且x1≤x2,均有对应的函数值f(x1)≤f(x2),则称函数f(x)在x取值范围内是非减函数.已知函数f(x)当0≤x≤1时为非减函数,且满足以下三个条件:
①f(0)=0,②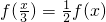 ,③f(1-x)=1-f(x);则
,③f(1-x)=1-f(x);则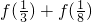 的值为
的值为
- A.

- B.

- C.

- D.1
C
分析:令x=1求出f( )的值,再令x=
)的值,再令x= 分别代入②③求出f(
分别代入②③求出f( )、f(
)、f( )的值,从而得解.
)的值,从而得解.
解答:令x=1,则f( )=
)= f(1),
f(1),
f(1-0)=1-f(0)=1,
所以,f( )=
)= ×1=
×1= ,
,
当x= 时,f(1-
时,f(1- )=1-f(
)=1-f( ),
),
所以,当f( )=1-f(
)=1-f( )=1-
)=1- =
= ,
,
所以,f( )=f(
)=f( ),
),
即函数关于x= 对称,
对称,
令x= ,则f(
,则f( )=f(
)=f( ×
× )=
)= f(
f( ),
),
当x= 时,f(1-
时,f(1- )=1-f(
)=1-f( ),
),
即f( )=1-f(
)=1-f( ),
),
∴f( )=
)= ,
,
∴f( )=
)= ×
× =
= ,
,
∴f( )+f(
)+f( )=
)= +
+ =
= .
.
故选C.
点评:本题考查了函数值求解,难度较大,关键在于求出关于x= 对称.
对称.
分析:令x=1求出f(
 )的值,再令x=
)的值,再令x= 分别代入②③求出f(
分别代入②③求出f( )、f(
)、f( )的值,从而得解.
)的值,从而得解.解答:令x=1,则f(
 )=
)= f(1),
f(1),f(1-0)=1-f(0)=1,
所以,f(
 )=
)= ×1=
×1= ,
,当x=
 时,f(1-
时,f(1- )=1-f(
)=1-f( ),
),所以,当f(
 )=1-f(
)=1-f( )=1-
)=1- =
= ,
,所以,f(
 )=f(
)=f( ),
),即函数关于x=
 对称,
对称,令x=
 ,则f(
,则f( )=f(
)=f( ×
× )=
)= f(
f( ),
),当x=
 时,f(1-
时,f(1- )=1-f(
)=1-f( ),
),即f(
 )=1-f(
)=1-f( ),
),∴f(
 )=
)= ,
,∴f(
 )=
)= ×
× =
= ,
,∴f(
 )+f(
)+f( )=
)= +
+ =
= .
.故选C.
点评:本题考查了函数值求解,难度较大,关键在于求出关于x=
 对称.
对称. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目

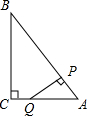 (2013•河西区一模)如图,Rt△ABC中,∠C=90°,AC=3,BC=4,P是斜边AB上一动点(不与点A、B重合),PQ⊥AB交△ABC的直角边于点Q,设AP为x,△APQ的面积为y,则下列图象中,能表示y关于x的函数关系的图象大致是( )
(2013•河西区一模)如图,Rt△ABC中,∠C=90°,AC=3,BC=4,P是斜边AB上一动点(不与点A、B重合),PQ⊥AB交△ABC的直角边于点Q,设AP为x,△APQ的面积为y,则下列图象中,能表示y关于x的函数关系的图象大致是( )