Question

【题目】如图，△ABC中，P为AB上的一点，在下列四个条件中：①∠ACP=∠B；②∠APC=∠ACB；③AC2=APAB；④ABCP=APCB，能满足△APC和△ACB相似的条件是（ ）

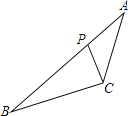
A．①②④ B．①③④ C．②③④ D．①②③

Answer 1

【答案】D

【解析】

试题分析：根据有两组角对应相等的两个三角形相似可对①②进行判断；根据两组对应边的比相等且夹角对应相等的两个三角形相似可对③④进行判断．

解：当∠ACP=∠B，

∠A公共，

所以△APC∽△ACB；

当∠APC=∠ACB，

∠A公共，

所以△APC∽△ACB；

当AC2=APAB，

即AC：AB=AP：AC，

∠A公共，

所以△APC∽△ACB；

当ABCP=APCB，即=，

而∠PAC=∠CAB，

所以不能判断△APC和△ACB相似．

故选D．