Question

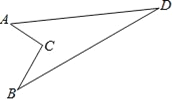
【题目】如图，有一块耕地ACBD，已知AD=24m，BD=26m，AC⊥BC，且AC=6m，BC=8m．求这块耕地的面积．

Answer 1

【答案】这块耕地的面积是96m2．

【解析】试题分析：连接AB，先根据勾股定理求出AB的长，再由勾股定理的逆定理，判断出△ABD的形状，根据S四边形ADBC=S△ABD﹣S△ABC即可得出结论．

试题解析：连接AB，

∵AC⊥BC，AC=6m，BC=8m，

∴Rt△ABC中，AB==10m，

∵AD=24m，BD=26m，

∴AD2=242=576，BD2=262=676，AB2=1002=100，

∴AB2+AD2=BD2，

∴△ABD是直角三角形，

∴S四边形ADBC=S△ABD﹣S△ABC=ABAD﹣ACBC=×10×24﹣×8×6=120﹣24=96m2．

答：这块耕地的面积是96m2．