Question

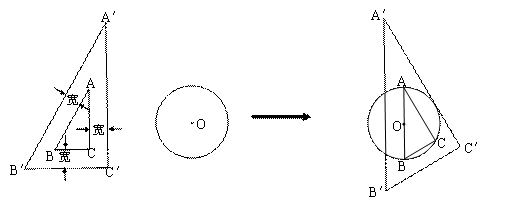
 (图1)为一锐角是30°的直角教学三角尺，其框为木质制成（内、外直角三角形对应边互相平行，且对应边之间的距离相等）．将三角尺移向直径为4㎝的⊙O，它的内Rt△ABC的斜边AB恰好等于⊙O的直径，它的外Rt△A′B′C′的直角边A′C恰好与⊙O相切（如图2），求直角三角尺（框）的宽和面积。

图1

Answer 1

解：宽：过O作OD⊥A′C′于D，交AC于E．             

        ∵AC∥A′C′

∴AC⊥OD       

∵A′C′与⊙O相切                                    

         ∴OD=OA=OB= 12AB=12×4=2（㎝）               

在Rt△AOE中,

∵∠A=30°

∴OE=12OA=12×2=1（㎝）                          

∴DE=OD－OE=2－1=1（㎝）                        

面积：=                                 

      延长AC交,于E,  F,

      ∴EF=

      ∴

      ∴=,       

  ∴框的面积为