题目内容
已知:图1为一锐角是30°的直角三角尺,其边框为透明塑料制成(内、外直角三角形对应边互相平行且三处所示宽度相等).
操作:将三角尺移向直径为4cm的⊙O,它的内Rt△ABC的斜边AB恰好等于⊙O的直径,它的外Rt△A′B′C′的直角边A′C′ 恰好与⊙O相切(如图2)。

思考:(1) 求直角三角尺边框的宽。
(2) 求 BB′C′+
BB′C′+ CC′B′的度数。
CC′B′的度数。
(3) 求边B′C′的长。
【答案】
(1) 2 (2) 75° (3)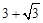
【解析】
试题分析:(1)如图2所示,将三角尺移向直径为4cm的⊙O,它的内Rt△ABC的斜边AB恰好等于⊙O的直径,即AB=4;图1为一锐角是30°的直角三角尺,内、外直角三角形对应边互相平行且三处所示宽度相等, ,根据直角三角形的性质,所以BC=
,根据直角三角形的性质,所以BC=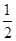 AB=2
AB=2
(2)因为内、外直角三角形对应边互相平行且三处所示宽度相等,它的外Rt△A′B′C′的直角边A′C′ 恰好与⊙O相切(如图2)。
由题意得BB′是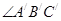 的角平分线,CC′是
的角平分线,CC′是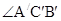 的角平分线,而
的角平分线,而 ,所以
,所以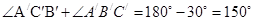 ;
;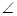 BB′C′+
BB′C′+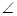 CC′B′=
CC′B′=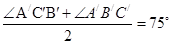
(3)过O点作OE⊥A1C1,过B点、C点作BE⊥B1C1,CF⊥B1C1于E、F两点
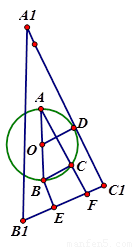
由题意知OA=OD=2, ,在直角三角形ABC中BC=
,在直角三角形ABC中BC=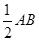 =2,四边形O1DC1F、BCEF是矩形,所以FC1=O1D,FC1=
=2,四边形O1DC1F、BCEF是矩形,所以FC1=O1D,FC1=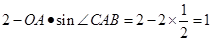 ;EF=BC=2;BB′是
;EF=BC=2;BB′是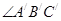 的角平分线,
的角平分线,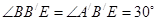 ,所以B1E=BB1
,所以B1E=BB1 =
=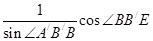 =
=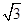 ,所以B′C′的长=1+2+
,所以B′C′的长=1+2+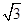 =3+
=3+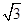
考点:圆、矩形,三角函数
点评:本题考查圆、矩形,三角函数,要求掌握圆的性质,矩形的性质,三角函数的定义,本题属中等难度题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,它的外Rt△A′B′C′的直角边A′C′恰好与⊙O相切(如图2).
,它的外Rt△A′B′C′的直角边A′C′恰好与⊙O相切(如图2).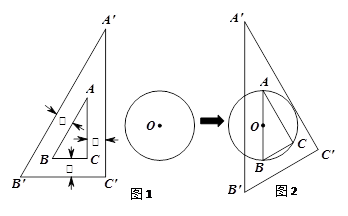
 CC′B′=75°。
CC′B′=75°。
 BB′C′+
BB′C′+
 BB′C′+
BB′C′+