题目内容
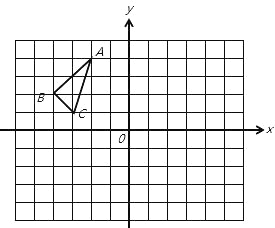
【题目】△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
(1)将△ABC向右移平2个单位长度,作出平移后的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)若将△ABC绕点(-1,0)顺时针旋转180°后得到△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)求出三角形ABC的面积
【答案】(1)A1(0,4),B1(-2,2),C1(-1,1)(2)A2(0,-4),B2(2,-2),C2(1,-1)(3)2
【解析】试题分析:
(1)先在坐标系描出平移后的A1、B1、C1,顺次连接这三点即可得到所求△A1B1C1,再写出A1、B1、C1三点的坐标即可;
(2)设点(-1,0)为点D,连接AD并延长至A2,使DA2=DA即可得到A2点,同法作出B2、C2,顺次连接三点即可得到△A2B2C2,再写出三点的坐标即可;
(3)如图2,由S△ABC=S矩形ADEF-S△ADB-S△BEC-S△ACF即可求出△ABC的面积.
试题解析:
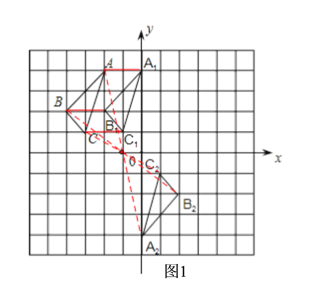
(1)如图1,图中△A1B1C1为所求三角形;三点的坐标分别为:A1(0,4),B1(-2,2),C1(-1,1);
(2)如图1,图中△A2B2C2为所求三角形;三点的坐标分别为:A2(0,-4),B2(2,-2),C2(1,-1);
(3)如图2,S△ABC=S矩形ADEF-S△ADB-S△BEC-S△ACF=![]() .
.


练习册系列答案
相关题目





