题目内容
【题目】如图,正方形OABC的面积为9,点O为左边原点,点A在![]() 轴上,点C在
轴上,点C在![]() 轴上,点B在函数
轴上,点B在函数![]() 的图象上,点P
的图象上,点P![]() 是函数
是函数![]() 图象上的任意一点,过点P分别作
图象上的任意一点,过点P分别作![]() 轴、
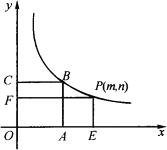
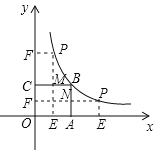
轴、![]() 轴的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合的部分(图中阴影部分)的面积为S.
轴的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合的部分(图中阴影部分)的面积为S.
(1)求B点坐标和![]() 值;
值;
(2)当![]() 时,求P点坐标.
时,求P点坐标.
【答案】(1)![]() ,
, ![]() ;(2)当
;(2)当![]() 时,P点坐标为
时,P点坐标为![]() 或
或![]() .
.
【解析】试题分析:(1)由正方形的面积,利用正方形的面积公式求出正方形的边长,确定出OA及AB的长,得到点B的坐标,将B的坐标代入反比例函数解析式中即可求出k值;
(2)分两种情况考虑:①当点P在点B的左边时,不重合部分为矩形PMCF,将P的坐标代入第一问确定出的反比例函数解析式中,得到mn的值,根据P及B的坐标,表示出PM与CM,利用矩形的面积公式表示出矩形PMCF的面积,将mn的值及已知的面积代入,即可求出m的值,进而得到n的值,确定出此时P的坐标;②当点P在点B的右边时,不重合部分为矩形ANPE,由P及B的坐标表示出AE及PE,利用矩形的面积公式表示出矩形ANPE的面积,将mn的值及已知的面积代入求出n的值,进而求出m的值,确定出此时P的坐标,综上,得到所有满足题意的P的坐标.
试题解析:解:(1)∵正方形OABC的面积为9,∴OA=OC=AB=BC=3,∴B(3,3).又∵点B(3,3)在函数![]() (k>0,x>0)的图象上,∴将B的坐标代入反比例函数解析式得:
(k>0,x>0)的图象上,∴将B的坐标代入反比例函数解析式得: ![]() =3,即k=9;
=3,即k=9;
(2)分两种情况:
①当点P在点B的左侧时,矩形OEPF和正方形OABC不重合部分为矩形PFCM.∵P(m,n)在函数![]() 上,∴mn=9.∵PE=n,ME=BA=3,∴PM=PE﹣ME=n﹣3,又CM=OE=m,∴S=CMPM=m(n﹣3)=mn﹣3m=9﹣3m=
上,∴mn=9.∵PE=n,ME=BA=3,∴PM=PE﹣ME=n﹣3,又CM=OE=m,∴S=CMPM=m(n﹣3)=mn﹣3m=9﹣3m=![]() ,解得:m=1.5,可得n=6,∴点P的坐标为(1.5,6);
,解得:m=1.5,可得n=6,∴点P的坐标为(1.5,6);
②当点P在点B的右侧时,矩形OEPF和正方形OABC不重合部分为矩形ANPE.∵P(m,n)在函数![]() 上,∴mn=9.∵OE=PF=m,NF=AO=3,
上,∴mn=9.∵OE=PF=m,NF=AO=3,![]() ,解得n=1.5,可得m=6,∴点P的坐标为(6,1.5).
,解得n=1.5,可得m=6,∴点P的坐标为(6,1.5).
综上所述:P的坐标为(1.5,6)或(6,1.5).

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案