��Ŀ����
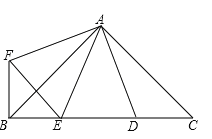
����Ŀ����ͼ����E�Ǿ���ABCD�ĶԽ���BD�ϵ�һ�㣬��BE=BC��AB=3��BC=4����PΪֱ��EC�ϵ�һ�㣬��PQ��BC�ڵ�Q��PR��BD�ڵ�R�� 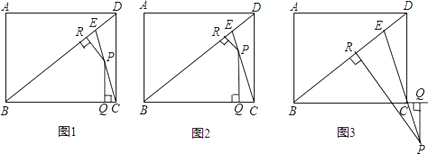
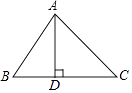
��1������ͼ1������PΪ�߶�EC�е�ʱ����֤��PR+PQ= ![]() ������֤������ ����ͼ2������PΪ�߶�EC�ϵ�����һ�㣨�����E����C�غϣ�ʱ�������������䣬����еĽ����Ƿ���Ȼ�������������������֤����������������˵�����ɣ�
������֤������ ����ͼ2������PΪ�߶�EC�ϵ�����һ�㣨�����E����C�غϣ�ʱ�������������䣬����еĽ����Ƿ���Ȼ�������������������֤����������������˵�����ɣ�
��2����ͼ3������PΪ�߶�EC�ӳ����ϵ�����һ��ʱ�������������䣬��PR��PQ֮���־���������������ϵ����ֱ��д����IJ��룮
���𰸡�
��1���⣺ͼ2�н���PR+PQ= ![]() �Գ�����
�Գ�����
֤��������BP����C����CK��BD�ڵ�K��
���ı���ABCDΪ���Σ�
���BCD=90�㣬
�֡�CD=AB=3��BC=4��
��BD= ![]() =5��
=5��
��S��BCD= ![]() BCCD=
BCCD= ![]() BDCK��
BDCK��
��3��4=5CK��
��CK= ![]() ��
��
��S��BCE= ![]() BECK��S��BEP=
BECK��S��BEP= ![]() PRBE��
PRBE��
S��BCP= ![]() PQBC����S��BCE=S��BEP+S��BCP��
PQBC����S��BCE=S��BEP+S��BCP��
�� ![]() BECK=
BECK= ![]() PRBE+
PRBE+ ![]() PQBC��
PQBC��
�֡�BE=BC��
�� ![]() CK=
CK= ![]() PR+
PR+ ![]() PQ��
PQ��
��CK=PR+PQ��
�֡�CK= ![]() ��
��
��PR+PQ= ![]() ��
��

��2���⣺��C��CF��BD��BD��F����CM��PR��PR��M������BP��
S��BPE��S��BCP=S��BEC��S��BEC�ǹ̶�ֵ��
BE=BCΪ�����ף�PR��PQ �ֱ�Ϊ�ߣ�ͼ3�еĽ�����PR��PQ= ![]()
����������1��������BP����C����CK��BD�ڵ�K�����ݾ��ε����ʼ����ɶ������BD�ij������������������ȿ����CK�ij������ͨ��������������֤������2��ͼ3�еĽ�����PR��PQ= ![]() ��
��
�����㾫����������Ҫ�����������ε�������ɶ����ĸ�������֪ʶ�㣬��Ҫ���������ε����=1/2���ס��ߣ�ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2������ȷ�����⣮

����Ŀ��������ABCD�ڲ������ɸ��㣬����Щ���Լ�������ABCD�Ķ���A��B��C��D��ԭ�����ηָ��һЩ������������ص�����

��1��������
������ABCD�ڵ�ĸ��� | 1 | 2 | 3 | 4 | �� | n |
�ָ�ɵ������εĸ��� | 4 | 6 | �� |
��2��ԭ�������ָܷ��2016�������Σ����ܣ����ʱ������ABCD�ڲ��ж��ٸ��㣿�����ܣ���˵��������