题目内容
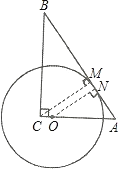
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4.动点O在边CA上移动,且⊙O的半径为2.
(1)若圆心O与点C重合,则⊙O与直线AB________; (2)当OC等于________时,⊙O与直线AB相切.

【答案】相离 ![]()
【解析】
(1)当圆心O与点C重合时,根据勾股定理求AB的长,利用“面积法”求点C到AB的距离,再与半径比较即可判断位置关系;
(2)作ON⊥AB,使ON=2,利用相似三角形的性质可求此时OC的长.
(1)作CM⊥AB,垂足为M
在Rt△ABC中,AB=![]() =5
=5
∵![]() ACBC=
ACBC=![]() ABCM
ABCM
∴CM=![]() ∵
∵![]() >2
>2
∴O与直线AB相离.
(2)如图,设O与AB相切,切点为N,连接ON
则ON⊥AB∴ON∥CM
∴△AON∽△ACM∴![]() =
=![]()
设OC=x,则AO=3x
∴![]() =
=![]() ∴x=
∴x=![]()
∴当CO=![]() 时,O与直线AB相切.
时,O与直线AB相切.

练习册系列答案
相关题目