题目内容
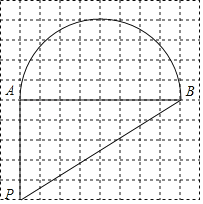
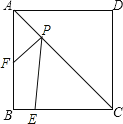
【题目】如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB的中点,P为AC上一个动点,则PF+PE的最小值为( )
A. 2![]() B. 4 C.
B. 4 C. ![]() D. 2
D. 2![]()
【答案】C
【解析】分析:
如下图,作点E关于直线AC的对称点E′,连接E′F,则E′F的长即为所求的PE+PF的最小值,过F作FG⊥CD于G,则CE′=CE=BC-BE=3,CG=BF=2,FG=BC=4,由此可得GE′=1,这样在Rt△FGE′中由勾股定理求出FE′的长即可.
详解:
作点E关于直线AC的对称点E′,连接E′F,则E′F的长即为所求的PE+PF的最小值,
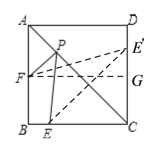
过F作FG⊥CD于G,则由题意可得CE′=CE,CG=BF,FG=BC,
∵BC=AB=4,BE=1,点F是AB的中点,
∴CE′=CE=BC-BE=3,CG=FB=2,FG=BC=4,
∴GE′=CE′-CG=3-2=1,
∴在Rt△E′FG中,E′F=![]() .
.
故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】地球运动是同学们非常喜欢的日常体育运动,为了更合理地配置体育运动器材和场地,某校针对“你最喜欢的球类运动”进行了一次随机抽样调查(每名被调查者分别选一项球类运动),并把调查结果绘制成如图的两个统计图表(不完整).
某校学生最喜爱的球类运动统计表
最喜爱的球类运动 | 人数 |
足球 | 27 |
篮球 |
|
乒乓球 | 24 |
羽毛球 | 24 |
排球 |
|
某校学生最喜爱的球类运动统计图

请根据所给信息,解答下列问题:
(1)本次被抽样调查的学生共有多少人?
(2)求扇形统计图中最喜爱篮球部分的圆心角度数;
(3)若该校共有学生960人,请根据抽样结果估计学生中最喜爱乒乓球的人数.