Question

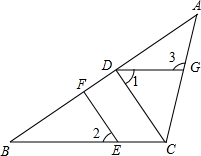如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F．
（1）CD与EF平行吗？为什么？
（2）如果∠1=∠2，且∠3=100°，求∠ACB的度数．

Answer 1

考点：平行线的判定与性质

专题：

分析：（1）先根据垂直的定义得到∠BFE=∠BDC=90°，然后根据同位角相等，两直线平行即可判断CD∥EF，
（2）由于CD∥EF，则∠2=∠BCD，利用∠1=∠2得到∠BCD=∠1，根据内错角相等，两直线平行判断DG∥BC，然后根据平行线的性质求解．

解答：解：（1）CD与EF平行．理由如下：
∵CD⊥AB，EF⊥AB，
∴∠BFE=∠BDC=90°，
∴CD∥EF（同位角相等，两直线平行），

（2）∵CD∥EF，
∴∠2=∠BCD（两直线平行，同位角相等），
∵∠1=∠2，
∴∠BCD=∠1，
∴DG∥BC（内错角相等，两直线平行），
∴∠ACB=∠3=100°（两直线平行，同位角相等）．

点评：本题考查了平行线的判定与性质：同位角相等，两直线平行；内错角相等，两直线平行；两直线平行，同位角相等．