题目内容
【题目】如图,在![]() 中,边
中,边![]() 的垂直平分线交
的垂直平分线交![]() 的平分线于点
的平分线于点![]() ,连接
,连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.

(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,则
,则![]() _______;(直接写出结果)
_______;(直接写出结果)
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)首先过点D作DE⊥OB于E,DF⊥OC于F,易证得△DEB≌△DFC(HL),即可得∠BDC=∠EDF,又由∠EOF+∠EDF=180°,即可求得答案;
(2)由(1),可求得∠BDC的度数.
(1)过点D作DE⊥OB,交OB延长线于点E,
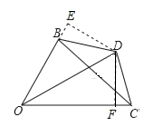
∵OD是∠BOC的平分线,
∴DE=DF,
∵DP是BC的垂直平分线,
∴BD=CD,
在Rt△DEB和Rt△DFC中,
![]() ,
,
∴△DEB≌△DFC(HL).
∴∠BDE=∠CDF,
∴∠BDC=∠EDF,
∵∠EOF+∠EDF=180°,
∵∠BOC=60°,
∴∠BDC=∠EDF=120°.
(2)∵∠EOF+∠EDF=180°,
∵∠BOC=α,
∴∠BDC=∠EDF=180°α.
故答案为:180°α.

练习册系列答案
相关题目
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.