Question

【题目】如图，在△ABC中，点D、E、F分别在BC、AB、AC上，且DE∥AC，DF∥AB．

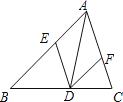
（1）如果∠BAC=90°，那么四边形AEDF是 形；

（2）如果AD是△ABC的角平分线，那么四边形AEDF是 形．

Answer 1

【答案】（1）矩．（2）菱.

【解析】

试题解析：（1）解：四边形AEDF是矩形，理由是：

∵DE∥AC，DF∥AB，

∴四边形AEDF是平行四边形，

∵∠BAC=90°，

∴平行四边形AEDF是矩形，

（2）解：四边形AEDF是菱形，理由是：

∵DE∥AC，DF∥AB，

∴四边形AEDF是平行四边形，

∵AD是△ABC的角平分线，

∴∠BAD=∠CAD，

∵DE∥AC，

∴∠EDA=∠CAD，

∴∠EDA=∠BAD，

∴AE=DE，

∴平行四边形AEDF是菱形