Question

【题目】已知：△ABC和△ADE均为等边三角形，连接BE，CD，点F，G，H分别为DE，BE，CD中点．

（1）当△ADE绕点A旋转时，如图1，则△FGH的形状为 ，说明理由；

（2）在△ADE旋转的过程中，当B，D，E三点共线时，如图2，若AB=3，AD=2，求线段FH的长；

（3）在△ADE旋转的过程中，若AB=a，AD=b（a＞b＞0），则△FGH的周长是否存在最大值和最小值，若存在，直接写出最大值和最小值；若不存在，说明理由．

Answer 1

【答案】（1）△FGH是等边三角形；（2）；（3）△FGH的周长最大值为（a+b），最小值为（a﹣b）．

【解析】试题（1）结论：△FGH是等边三角形．理由如下：根据三角形中位线定理证明FG=FH，再想办法证明∠GFH=60°即可解决问题；、

（2）如图2中，连接AF、EC．在Rt△AFE和Rt△AFB中，解直角三角形即可；

（3）首先证明△GFH的周长=3GF=BD，求出BD的最大值和最小值即可解决问题；

试题解析：解：（1）结论：△FGH是等边三角形．理由如下：

如图1中，连接BD、CE，延长BD交CE于M，设BM交FH于点O．

∵△ABC和△ADE均为等边三角形，∴AB=AC，AD=AE，∠BAC=∠DAE，∴∠BAD=∠CAE，∴△BAD≌△CAE，∴BD=CE，∠ADB=∠AEC，∵EG=GB，EF=FD，∴FG=BD，GF∥BD，∵DF=EF，DH=HC，∴FH=EC，FH∥EC，∴FG=FH，∵∠ADB+∠ADM=180°，∴∠AEC+∠ADM=180°，∴∠DMC+∠DAE=180°，∴∠DME=120°，∴∠BMC=60°

∴∠GFH=∠BOH=∠BMC=60°，∴△GHF是等边三角形，故答案为：等边三角形．

（2）如图2中，连接AF、EC．

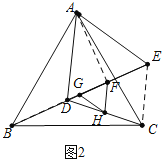
易知AF⊥DE，在Rt△AEF中，AE=2，EF=DF=1，∴AF==，在Rt△ABF中，BF= =，∴BD=CE=BF﹣DF=，∴FH=EC=．

（3）存在．理由如下．

由（1）可知，△GFH是等边三角形，GF=BD，∴△GFH的周长=3GF=BD，在△ABD中，AB=a，AD=b，∴BD的最小值为a﹣b，最大值为a+b，∴△FGH的周长最大值为（a+b），最小值为（a﹣b）．