题目内容
如图，半径为2的两个等圆与⊙O1外切于点P，过点O1作⊙O2的两条切线，切点分别为A，B，与⊙O1分别交于点C，D，则 |
| APB |
|
| CPD |
分析：分析：首先根据切线的性质得出∠AO1B=60°，∠A02B=120°，再根据弧长的计算公式是，就可以求出两条弧的长．
解答：解：连接O1O2，O2A，O2B
∵O1A是切线，∴O2A⊥O1A，
又∵O1O2=2O2A，∴∠AO1O2=30°，
∴∠AO1B=60°，∠A02B=120°，
CPD的弧长=
=
，APB的弧长=
=
，
∴APB与CPD的弧长之和为2π．
故选C．
∵O1A是切线，∴O2A⊥O1A，
又∵O1O2=2O2A，∴∠AO1O2=30°，
∴∠AO1B=60°，∠A02B=120°，
CPD的弧长=
| nπr |
| 180 |
| 2π |
| 3 |
| nπr |
| 180 |
| 4π |
| 3 |
∴APB与CPD的弧长之和为2π．
故选C．
点评：此题主要考查了切线的性质定理，利用三角函数求出圆心角，再根据弧长的公式求出弧长，求圆心角是解题的关键．
练习册系列答案
相关题目
如图，半径为2的两个等圆⊙O1，⊙O2外切于点A，O2C切⊙O1于点C，弦BC∥O1O2，连接AB，AC，则图中阴影部分的面积等于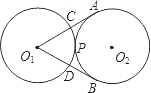
如图，半径为2的两个等圆⊙O1与⊙O2外切于点P，过O1作⊙O2的两条切线，切点分别为A，B，与⊙O1分别交于C，D，则APB与CPD的弧长之和为（ ）
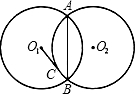如图，半径为5的两个等圆⊙O1与⊙O2相交于A、B，公共弦AB=8．由点O1向⊙O2作切线O1C，切点为C，则O1C的长为