题目内容
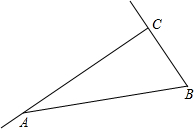 (2013•泉州质检)如图,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=5cm,点P从点C出发沿射线CA以每秒2cm的速度运动,同时点Q从点B出发沿射线BC以每秒1cm的速度运动.设运动时间为t秒.
(2013•泉州质检)如图,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=5cm,点P从点C出发沿射线CA以每秒2cm的速度运动,同时点Q从点B出发沿射线BC以每秒1cm的速度运动.设运动时间为t秒.(1)填空:AB=
5
| 5 |
5
cm;| 5 |
(2)若0<t<5,试问:t为何值时,△PCQ与△ACB相似;
(3)若∠ACB的平分线CE交△PCQ的外接圆于点E.试探求:在整个运动过程中,PC、QC、EC三者存在的数量关系式,并说明理由.
分析:(1)根据勾股定理求出即可;
(2)要使△PCQ与△ACB相似,必须有∠PQC=∠B或∠PQC=∠A成立.当∠PQC=∠A时,△PCQ∽△BCA,得出
=
,代入求出即可;当∠PQC=∠B时,△PCQ∽△ACB,得出
=
,代入求出即可;
(3)分为两种情况:画出图形,当0<t<5时,过点E作HE⊥CE交AC于H,求出∠HEP=∠CEQ,∠QCE=∠PCE=45°,PE=QE,证△QCE≌△PHE,推出QC=PH,根据勾股定理求出即可;当t≥5时,过点E作ME⊥CE交AC于M,同法可证△QCE≌△PME,根据勾股定理求出即可.
(2)要使△PCQ与△ACB相似,必须有∠PQC=∠B或∠PQC=∠A成立.当∠PQC=∠A时,△PCQ∽△BCA,得出
| CQ |
| CA |
| PC |
| BC |
| CQ |
| CB |
| PC |
| AC |
(3)分为两种情况:画出图形,当0<t<5时,过点E作HE⊥CE交AC于H,求出∠HEP=∠CEQ,∠QCE=∠PCE=45°,PE=QE,证△QCE≌△PHE,推出QC=PH,根据勾股定理求出即可;当t≥5时,过点E作ME⊥CE交AC于M,同法可证△QCE≌△PME,根据勾股定理求出即可.
解答:解:(1)在Rt△ABC中,∠ACB=90°,AB=10cm,BC=5cm,由勾股定理得:AB=
=5
(cm)
故答案为:5
;
(2)如图1,由题意可知:PC=2t,QB=t,QC=5-t.
∵∠PCQ=∠ACB,
∴要使△PCQ与△ACB相似,必须有∠PQC=∠B或∠PQC=∠A成立.
当∠PQC=∠A时,△PCQ∽△BCA,
由
=
可得
=
,
解得:t=1,
当∠PQC=∠B时,△PCQ∽△ACB,
由
=
可得
=
,
解得t=
,
∴当t=1或
秒时,△PCQ与△ACB相似;
(3)当0<t<5时,如图2,
过点E作HE⊥CE交AC于H,则∠HEP+∠PEC=90°,
∵∠ACB=90°,
∴PQ为△PCQ的外接圆的直径,
∴∠QEP=90°,即∠QEC+∠PEC=90°,
∴∠HEP=∠CEQ,
又∵CE平分∠ACB且∠ACB=90°,
∴∠QCE=∠PCE=45°,
∴
=
,
∴PE=QE,
∴∠QCE=∠PHE=45°,
∵在△QCE和△PHE中
 ∴△QCE≌△PHE(AAS)
∴△QCE≌△PHE(AAS)
∴QC=PH,
在Rt△HEC中,EC2+EH2=HC2,EC=EH,
即2EC2=(CP+CQ)2
∴CP+CQ=
EC;
当t≥5时,如图3,
过点E作ME⊥CE交AC于M,同法可证△QCE≌△PME,
∴CP-CQ=
EC,
综上所述,当0<t<5时,CP+CQ=
EC;当t≥5时,CP-CQ=
EC.
| 102+52 |
| 5 |
故答案为:5
| 5 |
(2)如图1,由题意可知:PC=2t,QB=t,QC=5-t.

∵∠PCQ=∠ACB,
∴要使△PCQ与△ACB相似,必须有∠PQC=∠B或∠PQC=∠A成立.
当∠PQC=∠A时,△PCQ∽△BCA,
由
| CQ |
| CA |
| PC |
| BC |
| 5-t |
| 10 |
| 2t |
| 5 |
解得:t=1,
当∠PQC=∠B时,△PCQ∽△ACB,
由
| CQ |
| CB |
| PC |
| AC |
| 5-t |
| 5 |
| 2t |
| 10 |
解得t=
| 5 |
| 2 |
∴当t=1或
| 5 |
| 2 |
(3)当0<t<5时,如图2,

过点E作HE⊥CE交AC于H,则∠HEP+∠PEC=90°,
∵∠ACB=90°,
∴PQ为△PCQ的外接圆的直径,
∴∠QEP=90°,即∠QEC+∠PEC=90°,
∴∠HEP=∠CEQ,
又∵CE平分∠ACB且∠ACB=90°,
∴∠QCE=∠PCE=45°,
∴
 |
| PE |
 |
| QE |
∴PE=QE,
∴∠QCE=∠PHE=45°,
∵在△QCE和△PHE中
|
 ∴△QCE≌△PHE(AAS)
∴△QCE≌△PHE(AAS)∴QC=PH,
在Rt△HEC中,EC2+EH2=HC2,EC=EH,
即2EC2=(CP+CQ)2
∴CP+CQ=
| 2 |
当t≥5时,如图3,
过点E作ME⊥CE交AC于M,同法可证△QCE≌△PME,
∴CP-CQ=
| 2 |
综上所述,当0<t<5时,CP+CQ=
| 2 |
| 2 |
点评:本题考查了等腰直角三角形,三角形的外接圆,相似三角形的性质和判定的应用,主要考查学生综合运用性质进行计算的能力,题目综合性比较强,难度偏大.

练习册系列答案
相关题目
 (2013•泉州质检)如图,由6个形状相同的小正方体搭成的一个几何体,此几何体的左视图是( )
(2013•泉州质检)如图,由6个形状相同的小正方体搭成的一个几何体,此几何体的左视图是( )