题目内容
如图,抛物线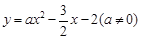 的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).
的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).
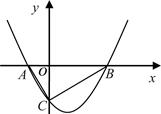
(1)求抛物线的解析式;
(2)判断△ABC的形状,说出△ABC外接圆的圆心位置,并求出圆心的坐标.
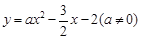 的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).
的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).
(1)求抛物线的解析式;
(2)判断△ABC的形状,说出△ABC外接圆的圆心位置,并求出圆心的坐标.
(1)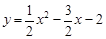 ;(2)该外接圆的圆心为AB的中点,且坐标为:
;(2)该外接圆的圆心为AB的中点,且坐标为: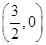 .
.
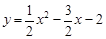 ;(2)该外接圆的圆心为AB的中点,且坐标为:
;(2)该外接圆的圆心为AB的中点,且坐标为: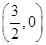 .
.试题分析:(1)该函数解析式只有一个待定系数,只需将B点坐标代入解析式中即可求解;
(2)首先根据抛物线的解析式确定A点、B点、C点坐标,然后通过证明△ABC是直角三角形来推导出直径AB和圆心的位置,由此确定圆心坐标.
试题解析:(1)∵点B(4,0)在抛物线
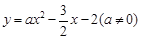 的图象上,∴
的图象上,∴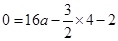 ,∴
,∴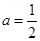 .∴抛物线的解析式为:
.∴抛物线的解析式为: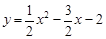 ;
;(2)△ABC为直角三角形.令x=0,得:y=-2,∴C(0,-2),令y=0,得
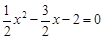 ,∴x1=-1,x2=4,∴A(-1,0),B(4,0),∴AB=5,AC=5BC=20,∴AC2+BC2=AB2,∴△ABC为直角三角形,∴AB为△ABC外接圆的直径,∴该外接圆的圆心为AB的中点,且坐标为:
,∴x1=-1,x2=4,∴A(-1,0),B(4,0),∴AB=5,AC=5BC=20,∴AC2+BC2=AB2,∴△ABC为直角三角形,∴AB为△ABC外接圆的直径,∴该外接圆的圆心为AB的中点,且坐标为: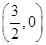 .
.考点: ①待定系数法求二次函数解析式;②勾股定理逆定理;③三角形的外心

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 的图像经过原点及点A(1,2),与x轴相交于另一点B.
的图像经过原点及点A(1,2),与x轴相交于另一点B.
 的解析式及B点坐标;
的解析式及B点坐标; 为对称轴向右翻折后,得到一个新的二次函数
为对称轴向右翻折后,得到一个新的二次函数 ,已知二次函数
,已知二次函数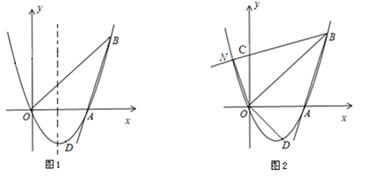

 有两个不同的实数根,方程
有两个不同的实数根,方程 也有两个不同的实数根,且其两根介于方程
也有两个不同的实数根,且其两根介于方程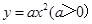 上向右跳动,得到点P2、P3,这时△P1P2P3的面积为 。
上向右跳动,得到点P2、P3,这时△P1P2P3的面积为 。
 ,则下列函数:①
,则下列函数:①
 ,②
,② ,③
,③ ,④
,④
 中,
中, 的值随
的值随 的值增大而增大的函数共有( )
的值增大而增大的函数共有( ) 个
个 个
个 个
个 个
个