题目内容
如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)请你求出点![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
(2)求出直线![]() 的解析式;
的解析式;
 (3
(3![]() )在抛物线上是否存在点
)在抛物线上是否存在点![]() ,使
,使![]() 的面积等于
的面积等于![]() 面积的3倍,若存在,请求出
面积的3倍,若存在,请求出![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
解:(1)当![]() 时,
时,![]() ………………………………………………1分
………………………………………………1分
![]() 当
当![]() 时,
时,![]()
解方程得:![]() ,
,![]() ……………………………………2分
……………………………………2分
∴它们的坐标是:![]() ,
,![]() ,
,![]() ………………3分
………………3分
(2)设![]() 的解析式是:
的解析式是:![]() ,则有
,则有
![]() …………………………………………………5分
…………………………………………………5分
解之得:![]()
∴所求的解析式是:![]() ……………………
……………………![]() ……………6分
……………6分
(3)存在点![]() ,使
,使![]() 的面积等于
的面积等于![]() 面积的3倍. ……7分
面积的3倍. ……7分
由![]() ,
,![]() 得:
得:![]() ,
,![]()
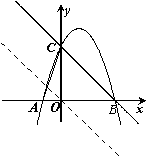 ∴
∴![]()
![]()
![]()
由![]() ,得:
,得:![]()
∴![]()
![]()
![]()
∴![]() ……………………………………………9分
……………………………………………9分
显然,在BC上方不存在点P. …………………………………………10分
过点![]() 作与直线
作与直线![]() 平行的直线,则可设这条直线的解析式为:
平行的直线,则可设这条直线的解析式为:![]()
由于此直线过点![]() ,则有:
,则有:![]()
∴这条平行线是:![]()
把![]() 代入
代入![]() 得:
得:
![]() ……………………………………………11分
……………………………………………11分
解之得:![]() ,
,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
∴所求的![]() 点坐标是:
点坐标是:![]() 和
和![]() …12分
…12分

练习册系列答案
相关题目

 的图象,其顶点坐标为M(1,-4).
的图象,其顶点坐标为M(1,-4).
 轴的交点A,B的坐标;
轴的交点A,B的坐标;  ,若存在,求出P点的坐标;若不存在,请说明理由;
,若存在,求出P点的坐标;若不存在,请说明理由; 与此图象有两个公共点时,
与此图象有两个公共点时, 的取值范围.
的取值范围.