题目内容
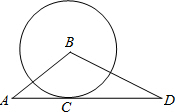如图，已知⊙B与△ABD的边AD相切于点C，AC=4，⊙B的半径为3，当⊙A与⊙B相切时，⊙A的半径是
- A.2
- B.7
- C.2或5
- D.2或8
D
分析：根据切线的性质可以求得BC的长，然后根据相切两圆的两种情况分类讨论即可．
解答：∵⊙B与△ABD的边AD相切于点C，AC=4，
∴BC=3，AB=5，
∵⊙A与⊙B相切，
∴当两圆外切时，⊙A的半径=5-3=2，
当两圆内切时，⊙A的半径=5+3=8．
故选D．
点评：本题考查了两圆之间的位置关系及勾股定理的知识，解题的关键是分类讨论，小心将另外一种情况漏掉．
分析：根据切线的性质可以求得BC的长，然后根据相切两圆的两种情况分类讨论即可．
解答：∵⊙B与△ABD的边AD相切于点C，AC=4，
∴BC=3，AB=5，
∵⊙A与⊙B相切，
∴当两圆外切时，⊙A的半径=5-3=2，
当两圆内切时，⊙A的半径=5+3=8．
故选D．
点评：本题考查了两圆之间的位置关系及勾股定理的知识，解题的关键是分类讨论，小心将另外一种情况漏掉．
练习册系列答案
相关题目
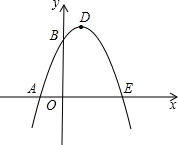如图，已知抛物线与x轴交于A（-1，0）、E（3，0）两点，与y轴交于点B（0，3）．
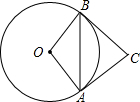如图，已知⊙O与CA、CB相切于点A、B，OA=OB=2
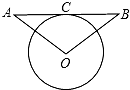（2012•市南区模拟）如图，已知AB与⊙O相切与点C，OA=OB，⊙O的直径为8cm，AB=6cm，则OA=
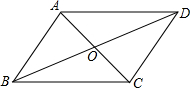如图，已知AC与BD相交于点O，OA=OC，OB=OD，则图中有多少对三角形全等（ ）
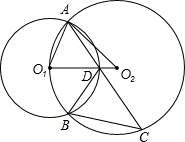如图，已知⊙O1与⊙O2的半径分别为r1，r2，⊙O2经过⊙O1的圆心O1，且两圆相交于A，B两点，C为⊙O2上的点，连接AC交⊙O1于D点，再连接BC，BD，AO1，AO2，O1O2，有如下四个结论：①∠BDC=∠AO1O2；②