题目内容
【题目】在平行四边形ABCD中,P为对角线BD上任意一点,连接PA、PC,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是![]() 、
、![]() 、
、![]() 、
、![]() ,给出如下结论:
,给出如下结论:
①![]() ②
②![]() ③
③![]() ④
④![]()
其中正确结论的序号是____________.(在横线上填上你认为所有正确答案的序号)

【答案】①③④
【解析】根据平行四边形的对边相等可得AB=CD,AD=BC,设点P到AB、BC、CD、DA的距离分别为h1、h2、h3、h4,然后利用三角形的面积公式列式整理即可判断出①正确;根据三角形的面积公式即可判断②③错误;根据已知进行变形,求出S1+S4=S2+S3=S△ABD=S△BDC=![]() S平行四边形ABCD,即可判断④.
S平行四边形ABCD,即可判断④.
∵四边形ABCD是矩形,∴AB=CD,AD=BC,
设点P到AB、BC、CD、DA的距离分别为h1、h2、h3、h4,
则S1=![]() ABh1,S2=
ABh1,S2=![]() BCh2,S3=
BCh2,S3=![]() CDh3,S4=
CDh3,S4=![]() ADh4,
ADh4,
∵![]() ABh1+
ABh1+![]() CDh3=
CDh3=![]() ABBC,
ABBC,![]() BCh2+
BCh2+![]() ADh4=
ADh4=![]() ABCD,
ABCD,
∴S2+S4=S1+S3,故①正确;
根据S4>S2只能判断h4>h2,不能判断h3>h1,即不能得出S3>S1,∴②错误;
根据S3=2S1,能得出h3=2h1,不能推出h4=2h2,即不能推出S4=2S2,∴③错误;
∵S1-S2=S3-S4,
∴S1+S4= S2+S3=![]() S平行四边形ABCD,
S平行四边形ABCD,
如图所示: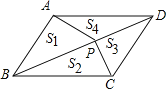
此时S1+S4=S2+S3=S△ABD=S△BDC=![]() S平行四边形ABCD,
S平行四边形ABCD,
即P点一定在对角线BD上,∴④正确;
故选D.
“点睛”本题考查了矩形的性质,三角形的面积,以及矩形对角线上点的判定的应用,用矩形的面积表示出相对的两个三角形的面积的和是解题的关键,也是本题的难点.

【题目】八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是分,乙队成绩的众数是分;
(2)计算甲、乙队的平均成绩和方差,试说明成绩较为整齐的是哪一队?
