题目内容
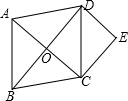 如图,O是菱形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE,CE交于点E.
如图,O是菱形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE,CE交于点E.(1)求证:四边形OCED是矩形;
(2)若菱形ABCD的周长为20,矩形OCED的周长为14,求菱形ABCD的面积.
分析:(1)易证四边形OCED为平行四边形,菱形对角线互相垂直,根据有一个内角为90°的平行四边形可以证明四边形为矩形;(2)根据菱形的周长可以求得菱形的边长,根据矩形的周长计算菱形对角线长,即可计算菱形的面积,即可解题.
解答:解:(1)∵DE∥AC,CE∥BD
∴四边形OCED为平行四边形,
∵AC,BD为菱形的对角线,
∴AC⊥BD,即∠COD=90°,
∴平行四边形OCED为矩形.
(2)菱形ABCD的周长为20,
则菱形的边长为5,即
=5,
矩形OCED的周长为14,
则OC+OD=7,
解题OC=3,OD=4,
∴AC=6,BD=8,
∴菱形的面积为
×6×8=24.
答:菱形ABCD的面积为 24.
∴四边形OCED为平行四边形,
∵AC,BD为菱形的对角线,
∴AC⊥BD,即∠COD=90°,
∴平行四边形OCED为矩形.
(2)菱形ABCD的周长为20,
则菱形的边长为5,即
| OC2+OD2 |
矩形OCED的周长为14,
则OC+OD=7,
解题OC=3,OD=4,
∴AC=6,BD=8,
∴菱形的面积为
| 1 |
| 2 |
答:菱形ABCD的面积为 24.
点评:本题考查了菱形对角线互相垂直平分的性质,考查了矩形的判定,考查了菱形各边长相等的性质,本题中根据OC,OD的关系求得OC,OD的值是解题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 ( )
( ) 时,菱形ABCD的边长为2.
时,菱形ABCD的边长为2.
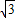 时,菱形ABCD的边长为2.
时,菱形ABCD的边长为2.
 时,菱形ABCD的边长为2.
时,菱形ABCD的边长为2.
 时,菱形ABCD的边长为2.
时,菱形ABCD的边长为2.