题目内容

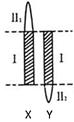
如果表示a，b两个实数的点在数轴上的位置如图所示，那么化简|a-b|+
(a+b)2
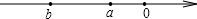
的结果等于（　　）精英家教网
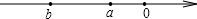
A、-2bB、2b
C、-2aD、2a
分析：由数轴可判断出a-b＞0，a+b＜0，然后再根据这两个条件对式子化简．
解答：解：由数轴可判断出a-b＞0，a+b＜0，
∴|a-b|+
(a+b)2
=a-b+|a+b|
=a-b-（a+b）=-2b．故选A．
点评：主要考查绝对值性质二次根式性质的运用．解此类题的关键是：先利用条件判断出绝对值符号里代数式的正负性，再根据绝对值的性质把绝对值符号去掉，把式子化简，即可求解．本题要注意二次根式
a2
的性质：当a≥0时，
a2
=a；a≤0时，
a2
=-a．
练习册系列答案
相关题目
28、如图1所示，长方形是由两个正方形拼成的，正方形的边长为a，对角线为b，长方形对角线为c．一只蚂蚁从A点爬形到C点．
（1）求蚂蚁爬形的最短路线长（只能按箭头所示的三条路线走），并说明理由；
（2）如果把右边的正方形EFBC沿EF翻转90°得到如图2所示的正方体相邻的两个面（实线表示），则蚂蚁从A点到C点的最短路线长是多少？请在图2中画出路线图，若与图中的线段有交点，则要标明并说明交点的准确位置．（可测量猜想判断）
阅读理解题：
定义：如果一个数的平方等于-1，记为i2=-1，这个数i叫做虚数单位．那么和我们所学的实数对应起来就叫做复数，表示为a+bi（a，b为实数），a叫这个复数的实部，b叫做这个复数的虚部，它的加，减，乘法运算与整式的加，减，乘法运算类似．
例如计算：（2+i）+（3-4i）=5-3i．
（1）填空：i3=
 
，i4=
 
．
（2）计算：①（2+i）（2-i）；②（2+i）2；
（3）若两个复数相等，则它们的实部和虚部必须分别相等，完成下列问题：已知：（x+y）+3i=（1-x）-yi，（x，y为实数），求x，y的值．
（4）试一试：请利用以前学习的有关知识将
1+i1-i
化简成a+bi的形式．
（18分）请回答下列Ⅰ、Ⅱ小题
Ⅰ、（8分）图甲表示在光照充足、CO2浓度适宜的条件下，温度对某植物真正光合作用速率和呼吸作用速率的影响。其中实线表示真正光合作用速率，虚线表示呼吸作用速率。图乙为该植物在适宜条件下，光合作用速率随光照强度变化的示意图。请据图回答：

（1）由图甲可知，与             作用有关的酶对高温更为敏感。温度会影响光合作用的                          阶段。
（2）当环境温度为40℃时，该植物的有机物净积累量为        mg/h。理论上预计，在温度为        条件下，植物生长状况达到最佳，已知乙图是在此温度条件下绘制而成的曲线，理论上分析，如果温度改变为45℃，图中b点将向        移。
（3）乙图中用                                     的量表示植物的光合作用速率，图中c点表示                                 
（4）乙图曲线中，当光照强度为0时，叶肉细胞中产生ATP的细胞器有              。
Ⅱ、（10分）大麻是一种雌雄异株的植物，请回答以下问题：

（1）在大麻体内，物质B的形成过程如右图所示，基因Mm和Nn分别位于两对常染色体上。
①据图分析，能产生B物质的大麻基因型可能有           种。
②如果两个不能产生B物质的大麻品种杂交，F1全都能产生B物质，则亲本的基因
型是                  和                 。F1中雌雄个体随机相交，后代中
能产生B物质的个体数和不能产生B物质的个体数之比应为              。
（2）右图为大麻的性染色体示意图，X、Y染色体的同源部分（图中I片断）上的基因互为等位，非同源部分（图中Ⅱ1、Ⅱ2片断）上的基因不互为等位。若大麻的抗病性状受性染色体上的显性基因D控制，大麻的雌、雄个体均有抗病和不抗病类型。请回答：

①控制大麻抗病性状的基因不可能位于右图中的        　   片段。
②请写出具有抗病性状的雄性大麻个体可能有的基因型      　　 。
③现有雌性不抗病和雄性抗病两个品种的大麻杂交，请根据以下子代可能出现的情
况，分别推断出这对基因所在的片段：
如果子代全为抗病，则这对基因位于 　   　 片段。
如果子代雌性全为不抗病，雄性全为抗病，则这对基因位于  　       片段。
如果子代雌性全为抗病，雄性全为不抗病，则这对基因位于     　           片
段。

如图1所示，长方形是由两个正方形拼成的，正方形的边长为a，对角线为b，长方形对角线为．一只蚂蚁从A点爬形到C点．

（1）求蚂蚁爬形的最短路线长（只能按箭头所示的三条路线走），并说明理由．

（2）如果把右边的正方形EFBC沿EF翻转90°得到如图2所示的正方体相邻的两个面（实线表示），则蚂蚁从A点到C点的最短路线长是多少？请在图2中画出路线图，若与图中的线段有交点，则要标明并说明交点的准确位置．（可测量猜想判断）

 


                   

如图所示，长方形是由两个正方形拼成的，正方形的边长为a，对角线为b，长方形对角线为．一只蚂蚁从A点爬形到C点．

（1）求蚂蚁爬形的最短路线长（只能按箭头所示的三条路线走），并说明理由．

（2）如果把右边的正方形EFBC沿EF翻转90°得到如图2所示的正方体相邻的两个面（实线表示），则蚂蚁从A点到C点的最短路线长是多少？请在图2中画出路线图，若与图中的线段有交点，则要标明并说明交点的准确位置．（可测量猜想判断）

 


                   

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网