题目内容
3、如果等腰梯形的两底之差等于一腰，则该梯形的较小底角的度数是（ ）
分析：如图，等腰梯形ABCD中，AD∥BC，AB=CD，BC-AD=AB，过A点作AE∥CD，平移一腰，把问题转化到△ABE中，判断三角形的形状，然后根据三角形ABE的形状来计算该梯形的较小底角∠B的度数即可．
解答：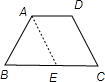
解：如图，梯形ABCD中，AD∥BC，AB=CD，BC-AD=AB，
过A点作AE∥CD，交BC于E点，
则AECD为平行四边形，
EC=AD，AE=CD，
∴AB=BC-AD=BC-CE=BE，
又∵AB=CD，
∴AB=BE=AE，
∴△ABE为等边三角形，
∴∠B=60°．
故选C．
解：如图，梯形ABCD中，AD∥BC，AB=CD，BC-AD=AB，过A点作AE∥CD，交BC于E点，
则AECD为平行四边形，
EC=AD，AE=CD，
∴AB=BC-AD=BC-CE=BE，
又∵AB=CD，
∴AB=BE=AE，
∴△ABE为等边三角形，
∴∠B=60°．
故选C．
点评：本题考查了等腰梯形的性质．平移一腰，能将梯形的两腰，上、下底的差，下底的两角，都集中在同一个三角形中，形成特殊三角形．
练习册系列答案
相关题目