题目内容
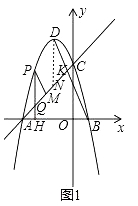
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2﹣2x+3与轴交于A、B两点,与y轴交于点C,点D为抛物线的顶点.
(1)求直线AC的解析式,并直接写出D点的坐标.
(2)如图1,在直线AC的上方抛物线上有一动点P,过P点作PQ垂直于x轴交AC于点Q,PM∥BD交AC于点M.
①求△PQM周长最大值;
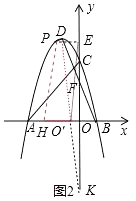
②当△PQM周长取得最大值时,PQ与x轴交点为H,首位顺次连接P、H、O、D构成四边形,它的周长为L,若线段OH在x轴上移动,求L最小值时OH移动的距离及L的最小值.
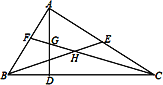
(3)如图2,连接BD与y轴于点F,将△BOF绕点O逆时针旋转,记旋转后的三角形为△BOF′,B′F′所在直线与直线AC、直线OC分别交于点G、K,当△CGK为直角三角形时,直接写出线段BG的长.

【答案】(1)、y=x+3;(﹣1,4);(2)、△PMQ的周长最大值为![]() ;L的最小值为
;L的最小值为![]() ;(3)、
;(3)、![]() 或4
或4![]()
【解析】
试题分析:(1)、首先求出抛物线与坐标轴的交点,利用待定系数法以及配方法即可解决问题.(2)、①如图1中,作DN∥y轴J交AC于N,直线BD交AC于K.先求出△DKN的三边,再求出PQ的最大值,利用相似三角形的性质求出PM、MQ即可解决问题.②如图2中,作PE∥x轴交y轴与E,作E关于x轴的对称点K,连接DK与x轴交于点O′,将OH平移到O′H处,此时四边形PHO′D的周长最小.分别求出PD,DK,OO′即可解决问题.(3)、分两种情形①如图3中,当∠CGK=90°时,作OE⊥GK于E,想办法求出点G坐标即可.②如图4中,当∠CKG=90°时,求出点G坐标即可解决问题.
试题解析:(1)、对于抛物线y=﹣x2﹣2x+3,令x=0得y=3,∴点C(0,3), 令y=0得﹣x2﹣2x+3=0,解得x=﹣3或1, ∴A(﹣3,0),B(1,0), 设直线AC的解析式为y=kx+b,把A、C两点坐标代入得到![]() , 解得
, 解得![]() , ∴直线AC的解析式为y=x+3.∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
, ∴直线AC的解析式为y=x+3.∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴顶点D坐标为(﹣1,4).
(2)、①如图1中,作DN∥y轴J交AC于N,直线BD交AC于K.
∵直线AC的解析式为y=x+3,直线BD的解析式为y=y=﹣2x+2, 由![]() 解得
解得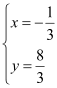 ,
,
∴点K坐标(﹣![]() ,
,![]() ),N(﹣1,2), ∴DN=2,DK=
),N(﹣1,2), ∴DN=2,DK= =
=![]() ,KN=
,KN= =
=![]() , 在△PMQ中,∵∠PMQ=∠DKN=定值,
, 在△PMQ中,∵∠PMQ=∠DKN=定值,
∴当△PMQ周长的最大值时,PQ定值最大,设P(m,﹣m2﹣2m+3)则Q(m,m+3),
∴PQ=﹣m2﹣2m+3﹣m﹣3=﹣m2﹣3m=﹣(m+![]() )2+
)2+![]() . ∵a=﹣1<0, ∴m=﹣
. ∵a=﹣1<0, ∴m=﹣![]() 时,PQ的最大值为
时,PQ的最大值为![]() ,
,
由△PMQ∽△DKN,得![]() =
=![]() =
=![]() , ∴
, ∴![]() =
=![]() =
=![]() , ∴PM=
, ∴PM=![]() ,MQ=
,MQ=![]() ,
,
∴△PMQ的周长最大值为![]() +
+![]() +
+![]() . ②如图2中,作PE∥x轴交y轴与E,作E关于x轴的对称点K,连接DK与x轴交于点O′,将OH平移到O′H处,此时四边形PHO′D的周长最小.
. ②如图2中,作PE∥x轴交y轴与E,作E关于x轴的对称点K,连接DK与x轴交于点O′,将OH平移到O′H处,此时四边形PHO′D的周长最小.
∵P(﹣![]() ,
,![]() ),D(﹣1,4),K(0,﹣
),D(﹣1,4),K(0,﹣![]() ), ∴O′坐标为(﹣
), ∴O′坐标为(﹣![]() ,0),PD=
,0),PD= =
=![]() ,DK=
,DK= =
=![]() ,O′H=
,O′H=![]() ,
,
∴OH向左平移![]() 个单位,L的最小值=PD+DK+O′H=
个单位,L的最小值=PD+DK+O′H=![]() +
+![]() +
+![]() .
.
()、①如图3中,当∠CGK=90°时,作OE⊥GK于E,
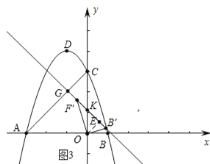
∵OA=OC,∠AOC=90°, ∴∠GCK=∠GKC=∠OKE=∠KOE=45°, ∵OE=![]() =
=![]() =
=![]() ,
,
∴OK=![]() ,KC=3﹣
,KC=3﹣![]() , ∴G(
, ∴G(![]() ﹣
﹣![]() ,
,![]() +
+![]() ),
),
∴GB= =
=![]() .
.
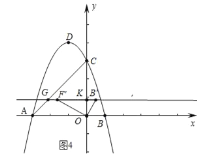
②如图4中,当∠CKG=90°时,点G(![]() ﹣3,
﹣3,![]() ),
),
∴BG= =4
=4![]() .
.

 阅读快车系列答案
阅读快车系列答案