题目内容
如图所示的两个圆盘中，指针落在每一个数所在的区域上的机会均等，则两个指针同时落在数“1”所在的区域上的概率是（ ）分析：首先根据题意列出表格，然后根据表格求得所有等可能的情况与两个指针同时落在数“1”所在的区域上的情况，然后利用概率公式求解即可求得答案．
解答：解：列表得：
∴一共有25种等可能的结果，两个指针同时落在数“1”所在的区域上的有1种情况，
∴两个指针同时落在数“1”所在的区域上的概率是：
．
故选A．
| （1，5） | （2，5） | （3，5） | （4，5） | （5，5） |
| （1，4） | （2，4） | （3，4） | （4，4） | （5，4） |
| （1，3） | （2，3） | （3，3） | （4，3） | （5，3） |
| （1，2） | （2，2） | （3，2） | （4，2） | （5，2） |
| （1，1） | （2，1） | （3，1） | （4，1） | （5，1） |
∴两个指针同时落在数“1”所在的区域上的概率是：
| 1 |
| 25 |
故选A．
点评：此题考查了列表法或树状图法求概率．解题的关键是注意列表法与树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；注意概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
如图所示的两个圆盘中，指针落在每一个数上的机会均等，那么两个指针同时落在偶数上的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
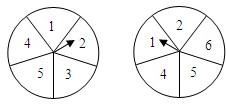
如图所示的两个圆盘中，指针落在每一个数上的机会均等，那么指针同时落在偶数的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
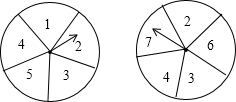如图所示的两个圆盘中，指针落在每一个数上的机会均等，那么两个指针同时指向奇数的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示的两个圆盘中，指针落在同一个圆盘的每一个区域的机会均等，则两个指针同时落在偶数区域的概率是（ ）