Question

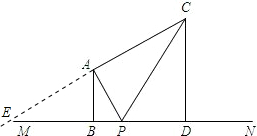
如图，已知AB⊥MN，垂足为点B，P是射线BN上的一个动点，AC⊥AP，∠ACP=∠BAP，AB=4，BP=x，CP=y，点C到MN的距离为线段CD的长．
（1）求y关于x的函数解析式，并写出它的定义域；
（2）在点P的运动过程中，点C到MN的距离是否会发生变化？如果发生变化，请用x的代数式表示这段距离；如果不发生变化，请求出这段距离；
（3）如果圆C与直线MN相切，且与以BP为半径的圆P也相切，求BP：PD的值．

Answer 1

（1）∵AB⊥MN，AC⊥AP，
∴∠ABP=∠CAP=90°．
又∵∠ACP=∠BAP，
∴△ABP∽△CAP．（1分）
∴

BP

AP

=

AP

PC

．
即

x

x2+16

=

x2+16

y

．（1分）
∴所求的函数解析式为y=

x2+16

x

（x＞0）．（1分）

（2）CD的长不会发生变化．（1分）
延长CA交直线MN于点E．（1分）
∵AC⊥AP，
∴∠PAE=∠PAC=90°．
∵∠ACP=∠BAP，
∴∠APC=∠APE．
∴∠AEP=∠ACP．
∴PE=PC．
∴AE=AC．（1分）
∵AB⊥MN，CD⊥MN，
∴AB∥CD．
∴

AB

CD

=

AE

CE

=

1

2

．（1分）
∵AB=4，
∴CD=8．（1分）

（3）∵圆C与直线MN相切，
∴圆C的半径为8．（1分）
（i）当圆C与圆P外切时，CP=PB+CD，即y=x+8，
∴

x2+16

x

=x+8，
∴x=2，（1分）
∴BP=2，
∴CP=y=2+8=10，
根据勾股定理得PD=6
∴BP：PD=

1

3

．（1分）
（ii）当圆C与圆P内切时，CP=|PB-CD|，即y=|x-8|，
∴

x2+16

x

=|x-8|．
∴

x2+16

x

=x-8或

x2+16

x

=8-x．
∴x=-2（不合题意，舍去）或无实数解．（1分）
∴综上所述BP：PD=

1

3

．