题目内容
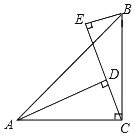
【题目】如图,等腰三角形ABC中,AB=AC=2,∠B=75°,以C为旋转中心将△ABC顺时针旋转,当点B落在AB上点D处时,点A的对应点为E,则阴影部分面积为_____.
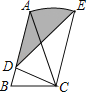
【答案】![]()
【解析】
作CK⊥BD于K.根据S阴=S△ABC+S扇形ACE﹣S△BCD﹣S△EDC计算即可.
解:作CK⊥BD于K.

∵AB=AC=3,
∴∠B=∠ACB=75°,
∴∠BAC=180°﹣75°﹣75°=30°,
在Rt△ACK中,CK=![]() AC=1,AK=
AC=1,AK=![]() ,
,
∴BK=2﹣![]() ,
,
∵CB=CD,CK⊥BD,
∴BD=2BK=4﹣2![]() ,∠B=∠CDB=75°,
,∠B=∠CDB=75°,
∴ACE=∠BCD=30°,
∴S阴=S△ABC+S扇形ACE﹣S△BCD﹣S△EDC
=![]() ﹣
﹣![]() (4﹣2
(4﹣2![]() )1
)1
=![]() ﹣2+
﹣2+![]() ,
,
故答案为![]() ﹣2+
﹣2+![]() .
.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
| ﹣4 |
| ﹣4 |
| 0 |
| … |
(1)求该抛物线的表达式;
(2)已知点E(4, y)是该抛物线上的点,点E关于抛物线的对称轴对称的点为点F,求点E和点F的坐标.