题目内容
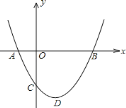
【题目】如图，二次函数
图象的顶点为D，其图象与x轴的交于点A、B，与y轴负半轴交于点C，且方程
的两根是-1和3.在下面结论中：①abc>0；②a+b+c<0；③c+3a=0；④若点M(
，m)在此抛物线上，则m小于c.正确的个数是( )
A.1个B.2个C.3个D.4个
【答案】D
【解析】
根据抛物线的开口方向、对称轴的位置和与y轴的交点位置即可判断出a、b、c的符合，从而判断①；再根据方程
的两根是-1和3，可求出点A坐标为（-1,0），点B坐标为（3,0），抛物线的对称轴为：直线x=
，从而求出抛物线上当x=1时，y＜0，
将x=1代入解析式即可判断a+b+c的符合，从而判断②；将x=-1和x=3分别代入方程中，用加减消元法消去b，即可判断③；根据抛物线的增减性即可判断④.
解:∵抛物线的开口向上
∴a＞0
∵对称轴在y轴右侧
∴a、b异号，即b＜0
∵抛物线与y轴交于负半轴
∴c＜0
∴abc＞0，①正确；
∵方程的两根是-1和3
∴点A坐标为（-1,0），点B坐标为（3,0），抛物线的对称轴为：直线x=
∴横坐标为1，且在抛物线上的点位于AB之间
由图可知：抛物线上当x=1时，y＜0
∴将x=1代入解析式中得y=a+b+c＜0，②正确；
将x=-1和x=3分别代入方程中得
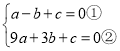
将①×3＋②得：12a＋4c=0
将等式两边同时除以4得：
3a+c=0，③正确；
由对称轴x=1可知：点C关于对称轴的对称点为（2，c）
而1＜
＜2
故此时C关于对称轴的对称点，M(，m)都在对称轴的右侧
由图像可知：对称轴右侧y随x增大而增大
∴m＜c，④正确；
故选D.
状元及第系列答案
同步奥数系列答案
【题目】某射击队教练为了了解队员训练情况，从队员中选取甲、乙两名队员进行射击测试，相同条件下各射靶5次，成绩统计如下：
命中环数 | 6 | 7 | 8 | 9 | 10 |
甲命中相应环数的次数 | 0 | 1 | 3 | 1 | 0 |
乙命中相应环数的次数 | 2 | 0 | 0 | 2 | 1 |
（1）根据上述信息可知：甲命中环数的中位数是_____环，乙命中环数的众数是______环；
（2）试通过计算说明甲、乙两人的成绩谁比较稳定？
（3）如果乙再射击1次，命中8环，那么乙射击成绩的方差会变小．（填“变大”、“变小”或“不变”）
