题目内容
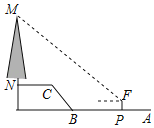
【题目】如图,MN是垂直于水平面的一棵树,小马(身高1.70米)从点A出发,先沿水平方向向左走2米到达P点处,在P处测得大树的顶端M的仰角为37°,再沿水平方向向左走8米到B点,再经过一段坡度i=4:3,坡长为5米的斜坡BC到达C点,然后再沿水平方向向左行走5米到达N点(A、B、C、N在同一平面内),则大树MN的高度约为( )(参考数据:tan37°≈0.75,sin37°≈0.60)
A.7.8米B.9.7米C.12米D.13.7米
【答案】B
【解析】
如图,作CD⊥AB于D,FH⊥MN于H.在Rt△MFH中,求出MH,再求出ON即可解决问题.
解:如图,作CD⊥AB于D,FH⊥MN于H.
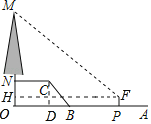
由题意四边形POHF,四边形ODCN都是矩形,
∴CN=OD=5m,CD=ON,OH=PF=1.70m,
在Rt△BCD中,∵CD:DB=4:3,BC=5m,
∴CD=ON=4m,DB=3m,
∵PB=8m,
∴HF=OP=OD+DB+PB=5+3+8=16,
在Rt△MFH中,MH=HFtan37°=16×0.75=12m,
∴MN=OM﹣ON=12+1.70﹣4=9.7m,
故选:B.

练习册系列答案
相关题目