题目内容
(2012•樊城区模拟)小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:
如图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知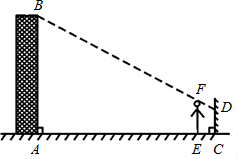 小明的身高EF是1.7m,则楼高AB=
小明的身高EF是1.7m,则楼高AB=
如图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知
 小明的身高EF是1.7m,则楼高AB=
小明的身高EF是1.7m,则楼高AB=20.0m
20.0m
.(结果精确到0.1m).分析:首先过点D作DG⊥AB,分别交AB、EF于点G、H,利用平行线的性质得出BG的长,进而得出AB的长即可.
解答: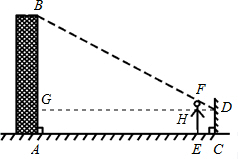 解:过点D作DG⊥AB,分别交AB、EF于点G、H,
解:过点D作DG⊥AB,分别交AB、EF于点G、H,
则EH=AG=CD=1.2,DH=CE=0.8,DG=CA=30,
∵EF∥AB,
∴
=
,
由题意,知FH=EF-EH=1.7-1.2=0.5,
则
=
,
解得,BG=18.75(m),
则AB=BG+AG=18.75+1.2=19.95≈20.0(m).
则楼高AB约为20.0米.
故答案为:20.0米.
 解:过点D作DG⊥AB,分别交AB、EF于点G、H,
解:过点D作DG⊥AB,分别交AB、EF于点G、H,则EH=AG=CD=1.2,DH=CE=0.8,DG=CA=30,
∵EF∥AB,
∴
| FH |
| BG |
| DH |
| DG |
由题意,知FH=EF-EH=1.7-1.2=0.5,
则
| 0.5 |
| BG |
| 0.8 |
| 30 |
解得,BG=18.75(m),
则AB=BG+AG=18.75+1.2=19.95≈20.0(m).
则楼高AB约为20.0米.
故答案为:20.0米.
点评:此题主要考查了相似三角形的应用,熟练掌握平行线分线段成比例的性质是解题关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
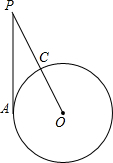 (2012•樊城区模拟)如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是⊙O上一点(点B与点A、C不重合),若∠APC=32°,求∠ABC的度数.
(2012•樊城区模拟)如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是⊙O上一点(点B与点A、C不重合),若∠APC=32°,求∠ABC的度数.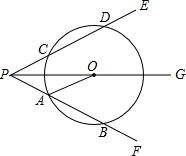 (2012•樊城区模拟)如图,O为∠EPF内射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A,B和C,D且AB=CD,连接OA,此时有OA∥PE.
(2012•樊城区模拟)如图,O为∠EPF内射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A,B和C,D且AB=CD,连接OA,此时有OA∥PE.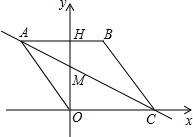 轴上,直线AC交y轴于点M,AB边交y轴于点H.
轴上,直线AC交y轴于点M,AB边交y轴于点H.