题目内容
(2012•樊城区模拟)如图,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(-3,4),点C在x轴的正半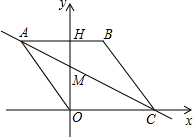 轴上,直线AC交y轴于点M,AB边交y轴于点H.
轴上,直线AC交y轴于点M,AB边交y轴于点H.
(1)求B、C两点坐标;
(2)抛物线y=
x2-bx+c经过A、O两点,求抛物线的解析式,并验证点C是否在抛物线上;
(3)在x轴上是否存在一点P,使△PCM与△ABC相似?若存在,求出点P的坐标;若不存在,请说明理由.
 轴上,直线AC交y轴于点M,AB边交y轴于点H.
轴上,直线AC交y轴于点M,AB边交y轴于点H.(1)求B、C两点坐标;
(2)抛物线y=
| 1 | 6 |
(3)在x轴上是否存在一点P,使△PCM与△ABC相似?若存在,求出点P的坐标;若不存在,请说明理由.
分析:(1)根据菱形的对边平行可得AB∥OC,然后求出∠AHO=∠COH=90°,在根据点A的坐标求出OH、AH的长度,然后利用勾股定理列式计算求出OA的长度,再求出BH的长度即可得到点B的坐标,根据菱形的边OC的长度可得点C的坐标;
(2)把点A、O的坐标代入抛物线解析式,解方程组求出b、c的值,即可得到抛物线解析式;然后把点C的坐标代入抛物线解析式,符合则点C在抛物线上;
(3)根据菱形的性质判定△AMH和△CMO相似,然后根据相似三角形对应边成比例列式求出MH与MO的比值,再根据OH的长度求出OM的长度,根据菱形的性质,△ABC是等腰三角形,所以①过点M作MP1∥BC交x轴于P1,利用两组角对应相等,两三角形相似可得△CMP1和△ACB相似,然后设OP1=m,表示出MP1,再利用勾股定理列出方程求解得到m的值,即可得到点P的坐标;②截取OP2=OC=5,根据线段垂直平分线上的点到线段两端点的距离相等可得MP2=MC,再根据等边对等角的性质以及菱形的性质可得∠MP2C=∠MCP2=∠ACB=∠BAC,然后得到△CP2M和△ACB相似,然后写出点P的坐标即可.
(2)把点A、O的坐标代入抛物线解析式,解方程组求出b、c的值,即可得到抛物线解析式;然后把点C的坐标代入抛物线解析式,符合则点C在抛物线上;
(3)根据菱形的性质判定△AMH和△CMO相似,然后根据相似三角形对应边成比例列式求出MH与MO的比值,再根据OH的长度求出OM的长度,根据菱形的性质,△ABC是等腰三角形,所以①过点M作MP1∥BC交x轴于P1,利用两组角对应相等,两三角形相似可得△CMP1和△ACB相似,然后设OP1=m,表示出MP1,再利用勾股定理列出方程求解得到m的值,即可得到点P的坐标;②截取OP2=OC=5,根据线段垂直平分线上的点到线段两端点的距离相等可得MP2=MC,再根据等边对等角的性质以及菱形的性质可得∠MP2C=∠MCP2=∠ACB=∠BAC,然后得到△CP2M和△ACB相似,然后写出点P的坐标即可.
解答:解:(1)在菱形ABCO中,OA=AB=BC=CO,AB∥OC,
所以,∠AHO=∠COH=90°,
∵点A的坐标为(-3,4),
∴OH=4,AH=3,
在Rt△AOH中,OA=
=
=5,
∴BH=5-3=2,
∴B(2,4)、C(0,5);
(2)把点A(-3,4)、O(0,0)代入抛物线解析式中得,
,
解得
,
所以,抛物线的解析式为y=
x2-
x,
当x=5时,y=
×52-
×5=0,
所以点C(5,0)在抛物线上;
(3)存在.理由如下:
在菱形ABCO中,AB∥OC,
∴∠BAC=∠OCA,
∠AHO=∠COH=90°,
∴△AMH∽△CMO,
∴
=
=
,
∵OH=4,
∴OM=
OH=2.5,
①过M作MP1∥BC交x轴于P1,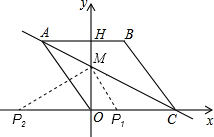
则∠CMP1=∠BCA,
∵∠BAC=∠OCA,
∴△CMP1∽△ACB,
在菱形ABCO中,∠ACB=∠ACO,
∴∠CMP1=∠ACO,
设OP1=m,则MP1=5-m,(m>0)
∴在Rt△MP1O中,
MP12=OP12+OM2,
即(5-m)2=m2+2.52,
解得m=1.875,
所以P1(1.875,0),
②截取OP2=OC=5,
∵OM⊥x轴,
∴MP2=MC,
∴∠MP2C=∠MCP2,
由上知:∠MP2C=∠MCP2=∠ACB=∠BAC,
∴△CP2M∽△ACB,
此时P2(-5,0),
综上所述,P点有两个,坐标为(1.875,0)和(-5,0).
所以,∠AHO=∠COH=90°,
∵点A的坐标为(-3,4),
∴OH=4,AH=3,
在Rt△AOH中,OA=
| OH2+AH2 |
| 42+32 |
∴BH=5-3=2,
∴B(2,4)、C(0,5);
(2)把点A(-3,4)、O(0,0)代入抛物线解析式中得,
|
解得
|
所以,抛物线的解析式为y=
| 1 |
| 6 |
| 5 |
| 6 |
当x=5时,y=
| 1 |
| 6 |
| 5 |
| 6 |
所以点C(5,0)在抛物线上;
(3)存在.理由如下:
在菱形ABCO中,AB∥OC,
∴∠BAC=∠OCA,
∠AHO=∠COH=90°,
∴△AMH∽△CMO,
∴
| MH |
| MO |
| AH |
| CO |
| 3 |
| 5 |
∵OH=4,
∴OM=
| 5 |
| 8 |
①过M作MP1∥BC交x轴于P1,

则∠CMP1=∠BCA,
∵∠BAC=∠OCA,
∴△CMP1∽△ACB,
在菱形ABCO中,∠ACB=∠ACO,
∴∠CMP1=∠ACO,
设OP1=m,则MP1=5-m,(m>0)
∴在Rt△MP1O中,
MP12=OP12+OM2,
即(5-m)2=m2+2.52,
解得m=1.875,
所以P1(1.875,0),
②截取OP2=OC=5,
∵OM⊥x轴,
∴MP2=MC,
∴∠MP2C=∠MCP2,
由上知:∠MP2C=∠MCP2=∠ACB=∠BAC,
∴△CP2M∽△ACB,
此时P2(-5,0),
综上所述,P点有两个,坐标为(1.875,0)和(-5,0).
点评:本题是二次函数综合题型,主要考查了菱形的性质,勾股定理的应用,待定系数法求二次函数解析式,相似三角形的判定,(3)因为相似三角形对应边不确定,所以要分情况讨论求解.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
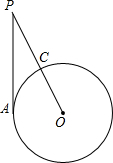 (2012•樊城区模拟)如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是⊙O上一点(点B与点A、C不重合),若∠APC=32°,求∠ABC的度数.
(2012•樊城区模拟)如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是⊙O上一点(点B与点A、C不重合),若∠APC=32°,求∠ABC的度数.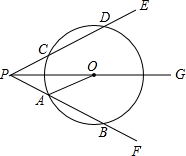 (2012•樊城区模拟)如图,O为∠EPF内射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A,B和C,D且AB=CD,连接OA,此时有OA∥PE.
(2012•樊城区模拟)如图,O为∠EPF内射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A,B和C,D且AB=CD,连接OA,此时有OA∥PE.