Question

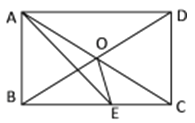
【题目】如图，矩形ABCD中，AE平分∠BAD交BC于E，∠CAE=15°，则下列结论①△ODC是等边三角形；②BC=2AB；③∠AOE=135°；④S△AOE=S△COE 其中正确的结论的序号是__________

Answer 1

【答案】①③④

【解析】∵矩形ABCD中，AE平分∠BAD, ∴∠BAE=45°, ∵∠CAE=15°, ∴∠BAO=∠BAE+∠CAE=45°+15°=60°,又∵矩形中OA=OB=OC=OD, ∴△AOB是等边三角形，∴∠AOB=∠COD=60°, ∴△ODC是等边三角形，故①正确；由等边三角形的性质，AB=OA, ∴AC=2AB,由垂线段最短BC<AC, ∴BC<2AB,故②错误；∵∠BAE=45°, ∠ABE=90°, ∴△ABE是等腰直角三角形，∴AB=BE,BO=BE, ∵∠COB=180°-60°=120°, ∴∠BOE= (180°-30°)=75°,

∴∠AOE=∠AOB+∠BOE=60°+75°=135°,故③正确；∵△AOE和△COE的底边AO=CO,点E到AC的距离相等，∴ ,故④正确；综上所述，正确的结论是①③④.

点睛:本题考查了矩形的性质，等边三角形的判定与性质，等腰三角形的性质，垂线段最短，等底等高的三角形的面积相等，综合题，但难度不大，熟记性质并准确识图理清图中各角度之间的关系是解题的关键.