题目内容
 如图,△ABC中,AB=BC=5,AC=3.D为AB上的点(点D与点A、B不重合),作DE∥BC交AC于点E.
如图,△ABC中,AB=BC=5,AC=3.D为AB上的点(点D与点A、B不重合),作DE∥BC交AC于点E.
(1)若CE=x,BD=y,求y与x的函数关系式,并写出自变量x的范围;
(2)若G为BC边上一点,当四边形DECG为菱形时,求BG的长;
(3)BC边上是否存在点F,使△FDE∽△BAC?若存在,请求出线段BF的长;若不存在,请说明理由.
解:(1)∵DE∥BC交AC于点E,
∴△ADE∽△ABC,
∴ ,
,
∵CE=x,BD=y,
∴AE=AC-CE=3-x,AD=AB-BD=5-y,
∴ ,
,
∴y= x(0<x<3);
x(0<x<3);
(2)∵四边形DECG为菱形,
∴DG∥AC,DE=DG=CG=CE,
∴△BGD∽△BCA,
∴ ,
,
设BG=a,则CG=5-a,
∴DG=CG=5-a,
∴ ,
,
∴a= ,
,
∴BG= ;
;
(3)BC边上存在点F,使△FDE∽△BAC,
∵△FDE∽△BAC,
∴∠DFE=∠ABC,∠FDE=∠BAC,∠DEF=∠ACB,
又∵DE∥BC,
∴∠DEF=∠EFC,
∴∠DFE=∠FEC,
∴DF∥AC,
∴四边形DFCE为平行四边形,
∴△BDF∽△BAC,
设DE=3k,则DF=EF=EC=5k,FC=3k
∴ ,
,
∴ ,
,
∴k=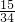 <6,
<6,
∴BF=5-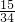 =
=
∴当BF= 时,△FDE∽△BAC.
时,△FDE∽△BAC.
分析:(1)由DE∥BC,可得△ADE∽△ABC,由相似三角形的性质:对应边的比值相等即可的到x和y的函数关系式,在由已知条件写出自变量x的范围即可;
(2)根据菱形的性质四边相等,可设BG=a,则CG=DG=5-a,又因为DG∥AC,所以△BGD∽△BCA,利用相似三角形的性质可得到关于a的比例式,求出a即可;
(3)假设BC边上存在点F,使△FDE∽△BAC当,由相似三角形的性质和已知条件可证明四边形DFCE为平行四边形,进而证明△BDF∽△BAC,设DE=3k,则DF=EF=EC=5k,FC=3k,由比例式即可求出k的值,若k<5即可存在,否则不存在.
点评:本题考查了相似三角形的判定和性质、平行四边形的判定和性质、菱形的性质,题目的综合性很强,解题的关键是设未知数建立方程,运用方程的思想解几何问题.
∴△ADE∽△ABC,
∴
 ,
,∵CE=x,BD=y,
∴AE=AC-CE=3-x,AD=AB-BD=5-y,
∴
 ,
,∴y=
 x(0<x<3);
x(0<x<3);(2)∵四边形DECG为菱形,
∴DG∥AC,DE=DG=CG=CE,
∴△BGD∽△BCA,
∴
 ,
,
设BG=a,则CG=5-a,
∴DG=CG=5-a,
∴
 ,
,∴a=
 ,
,∴BG=
 ;
;(3)BC边上存在点F,使△FDE∽△BAC,
∵△FDE∽△BAC,
∴∠DFE=∠ABC,∠FDE=∠BAC,∠DEF=∠ACB,
又∵DE∥BC,
∴∠DEF=∠EFC,
∴∠DFE=∠FEC,
∴DF∥AC,

∴四边形DFCE为平行四边形,
∴△BDF∽△BAC,
设DE=3k,则DF=EF=EC=5k,FC=3k
∴
 ,
,∴
 ,
,∴k=
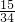 <6,
<6,∴BF=5-
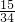 =
=
∴当BF=
 时,△FDE∽△BAC.
时,△FDE∽△BAC.分析:(1)由DE∥BC,可得△ADE∽△ABC,由相似三角形的性质:对应边的比值相等即可的到x和y的函数关系式,在由已知条件写出自变量x的范围即可;
(2)根据菱形的性质四边相等,可设BG=a,则CG=DG=5-a,又因为DG∥AC,所以△BGD∽△BCA,利用相似三角形的性质可得到关于a的比例式,求出a即可;
(3)假设BC边上存在点F,使△FDE∽△BAC当,由相似三角形的性质和已知条件可证明四边形DFCE为平行四边形,进而证明△BDF∽△BAC,设DE=3k,则DF=EF=EC=5k,FC=3k,由比例式即可求出k的值,若k<5即可存在,否则不存在.
点评:本题考查了相似三角形的判定和性质、平行四边形的判定和性质、菱形的性质,题目的综合性很强,解题的关键是设未知数建立方程,运用方程的思想解几何问题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.
26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB. 27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE.
27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE. 27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M
27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M 14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )
14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( ) 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.