题目内容
(2005•泉州质检)某公园出售的一次性使用门票,每张10元,同时又推出购买“个人年票”的售票方法(从购买日起,可供持票者使用一年),年票分A,B两类:A类年票每张100元,持票者每次进入公园无需再购买门票,B类年票每张40元,持票者每次进入公园时需再购买每次2元的门票.现有甲,乙,丙三位游客在一年中分别选择用A类年票,B类年票,一次性使用门票三种方式去游园,并且乙,丙每人一年中恰好都进入该公园x次.(1)请分别写出乙,丙每人一年的门票费支出(用含x的代数式表示);
(2)①在三位游客每人一年的门票费支出中,当甲的支出为最少时:乙,丙每人一年中进入该公园至少超过多少次?
②求此时三位游客一年中游园共支出的门票费总额的最小值.
【答案】分析:(1)根据题意直接列式即可;
(2)根据“乙一年的门票支出大于100”“丙一年的门票支出大于100”列不等式求解即可得x的范围;设此时三游客一年中游园共支出的门票总额为W元,则W可以表示成x的函数,根据函数的性质,就可以求出.
解答:解:(1)乙一年的门票支出为(40+20x)元(2分)
丙一年的门票支出为10x元(4分).
(2)①依题意得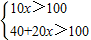 (6分)
(6分)
解得:x>30 (7分)
则乙丙两人一年中进入该公园至少超过30次(8分)
②设此时三位游客一年中游园共支出的门票总额为W元
则W=100+40+2x+10x
=12x+140(x>30,且x为正整数) (10分)
∵w随x的增大而增大(11分)
∴当x=31时
w的最小值为12×31+140=512元
∴此时三位游客一年中游园共支出的门票费的最小值为512元(13分)
点评:本题考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.要会根据自变量的取值范围结合函数的单调性求函数的最值问题.
(2)根据“乙一年的门票支出大于100”“丙一年的门票支出大于100”列不等式求解即可得x的范围;设此时三游客一年中游园共支出的门票总额为W元,则W可以表示成x的函数,根据函数的性质,就可以求出.
解答:解:(1)乙一年的门票支出为(40+20x)元(2分)
丙一年的门票支出为10x元(4分).
(2)①依题意得
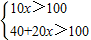 (6分)
(6分)解得:x>30 (7分)
则乙丙两人一年中进入该公园至少超过30次(8分)
②设此时三位游客一年中游园共支出的门票总额为W元
则W=100+40+2x+10x
=12x+140(x>30,且x为正整数) (10分)
∵w随x的增大而增大(11分)
∴当x=31时
w的最小值为12×31+140=512元
∴此时三位游客一年中游园共支出的门票费的最小值为512元(13分)
点评:本题考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.要会根据自变量的取值范围结合函数的单调性求函数的最值问题.

练习册系列答案
相关题目
 .
.
 .
.