题目内容
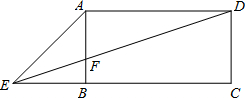 (2012•顺义区二模)如图,在矩形ABCD中,E是边CB延长线上的点,且EB=AB,DE与AB相交于点F,AD=2,CD=1,求AE及DF的长.
(2012•顺义区二模)如图,在矩形ABCD中,E是边CB延长线上的点,且EB=AB,DE与AB相交于点F,AD=2,CD=1,求AE及DF的长.分析:利用矩形的性质、勾股定理求得AE的长度;然后在Rt△DCE中根据平行线分线段成比例可知EF、DF间的数量关系;最后利用线段ED与EF、DF间的和差关系即可求得DF的长度.
解答:解:∵四边形ABCD是矩形,且AD=2,CD=1,
∴BC=AD=2,AB=CD=1,∠ABC=∠C=90°,AB∥DC.
∴EB=AB=1.
在Rt△ABE中,AE=
=
;
在Rt△DCE中,DE=
=
=
;
∵AB∥DC,
∴
=
=
.
设EF=x,则DF=2x.
∵EF+DF=DE,
∴x+2x=
∴x=
,
∴DF=2x=
.
∴BC=AD=2,AB=CD=1,∠ABC=∠C=90°,AB∥DC.
∴EB=AB=1.
在Rt△ABE中,AE=
| AB2+BE2 |
| 2 |
在Rt△DCE中,DE=
| DC2+CE2 |
| 12+32 |
| 10 |
∵AB∥DC,
∴
| EF |
| DF |
| EB |
| BC |
| 1 |
| 2 |
设EF=x,则DF=2x.
∵EF+DF=DE,
∴x+2x=
| 10 |
∴x=
| ||
| 3 |
∴DF=2x=
| 2 |
| 3 |
| 10 |
点评:本题考查了勾股定理、矩形的性质以及平行线分线段成比例.利用平行线分线段成比例定理时,要找准对应关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
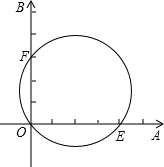 (2012•顺义区二模)如图,小华同学设计了一个圆直径的测量器,把标有刻度的尺子OA、OB在O点钉在一起,并使它们保持互相垂直.在测直径时,把O点靠在圆周上,读得刻度OE=4个单位,OF=3个单位,则圆的直径为( )
(2012•顺义区二模)如图,小华同学设计了一个圆直径的测量器,把标有刻度的尺子OA、OB在O点钉在一起,并使它们保持互相垂直.在测直径时,把O点靠在圆周上,读得刻度OE=4个单位,OF=3个单位,则圆的直径为( )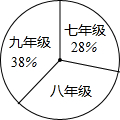 图,其中八年级学生人数为204人,请你根据图表中提供的信息,解答下列问题:
图,其中八年级学生人数为204人,请你根据图表中提供的信息,解答下列问题: