题目内容
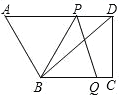
【题目】如图,在平行四边形ABCD中,O是AB的中点,连接DO并延长交CB的延长线于点E,连接AE、DB.
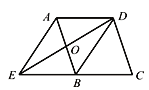
(1)求证:△AOD≌△BOE;
(2)若DC=DE,判断四边形AEBD的形状,并说明理由.
【答案】(1)证明见解析;(2)四边形AEBD是矩形.
【解析】
(1)利用平行线得到∠ADO=∠BEO,再利用对顶角相等和线段中点,可证明△AOD≌△BOE;
(2)先证明四边形AEBD是平行四边形,再利用对角线相等的平行四边形的矩形,可判定四边形AEBD是矩形.
(1)∵四边形ABCD是平行四边形,∴AD∥CE,∴∠ADO=∠BEO.
∵O是BC中点,∴AO=BO.
又∵∠AOD=∠BOE,∴△AOD≌△BOE(AAS);
(2)四边形AEBD是矩形,理由如下:
∵△AOD≌△BOE,∴DO=EO.
又AO=BO,∴四边形AEBD是平行四边形.
∵DC=DE=AB,∴四边形AEBD是矩形.

练习册系列答案
相关题目