题目内容
已知一元二次方程x2+px+q=0的两根是-1和2,则抛物线y=x2+px+q的顶点坐标是________.
( ,-
,- )
)
分析:先把两根代入一元二次方程x2+px+q=0求得p、q的值,再将p、q代入y=x2+px+q,最后求顶点坐标.
解答:∵一元二次方程x2+px+q=0的两根是-1和2,
∴-1和2满足一元二次方程x2+px+q=0,
∴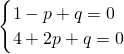 ,
,
解得,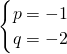 ;
;
∴y=x2-x-2,即y=(x- )2-
)2- ,
,
∴抛物线y=x2+px+q的顶点坐标是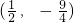 .
.
故答案为:( ,-
,- ).
).
点评:本题主要考查了一元二次方程的解的意义及二次函数的图象的特点.二次函数y=a(x-h)2+k,它的顶点坐标及对称轴如下:
顶点坐标(h,k);对称轴x=h;因此,研究抛物线y=ax2+bx+c(a≠0)的图象,通过配方,将一般式化为y=a(x-h)2+k的形式,可确定其顶点坐标、对称轴,抛物线的大体位置就很清楚了.这给画图象提供了方便.
 ,-
,- )
)分析:先把两根代入一元二次方程x2+px+q=0求得p、q的值,再将p、q代入y=x2+px+q,最后求顶点坐标.
解答:∵一元二次方程x2+px+q=0的两根是-1和2,
∴-1和2满足一元二次方程x2+px+q=0,
∴
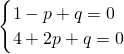 ,
,解得,
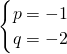 ;
;∴y=x2-x-2,即y=(x-
 )2-
)2- ,
,∴抛物线y=x2+px+q的顶点坐标是
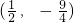 .
.故答案为:(
 ,-
,- ).
).点评:本题主要考查了一元二次方程的解的意义及二次函数的图象的特点.二次函数y=a(x-h)2+k,它的顶点坐标及对称轴如下:
顶点坐标(h,k);对称轴x=h;因此,研究抛物线y=ax2+bx+c(a≠0)的图象,通过配方,将一般式化为y=a(x-h)2+k的形式,可确定其顶点坐标、对称轴,抛物线的大体位置就很清楚了.这给画图象提供了方便.

练习册系列答案
相关题目