题目内容
 (2013•同安区一模)如图,矩形ABCD中,从较短边AD上找一点E,过点E剪下一个正三角形和一个正方形,它们边长分别为DE和AE.设矩形相邻两边长分别为6和
(2013•同安区一模)如图,矩形ABCD中,从较短边AD上找一点E,过点E剪下一个正三角形和一个正方形,它们边长分别为DE和AE.设矩形相邻两边长分别为6和| 3 |
4
4
时,使得剪下的正三角形的面积和正方形的面积之和最小,最小值为4
+3
| 3 |
4
+3
.| 3 |
分析:设DE=x,则AE=
+4-x,剪下的正三角形的面积和正方形的面积之和为y,根据正三角形和正方形的面积公式得y=
x2+(
+4-x)2,整理后发现y是x的二次函数,根据二次函数的性质即可求解.
| 3 |
| ||
| 4 |
| 3 |
解答:解:设DE=x,则AE=
+4-x,剪下的正三角形的面积和正方形的面积之和为y,
由题意,得y=
x2+(
+4-x)2
=
x2+3+16+x2+8
-2
x-8x
=(
+1)x2-(2
+8)x+(19+8
),
∵
+1>0,
∴当x=
=4时,y有最小值,
最小值是:
=4
+3.
故答案为4,4
+3.
| 3 |
由题意,得y=
| ||
| 4 |
| 3 |
=
| ||
| 4 |
| 3 |
| 3 |
=(
| ||
| 4 |
| 3 |
| 3 |
∵
| ||
| 4 |
∴当x=
2
| ||||
2(
|
最小值是:
4(
| ||||||||
4(
|
| 3 |
故答案为4,4
| 3 |
点评:本题考查了正三角形和正方形的面积,二次函数的性质,二次根式的化简,难度适中,得出y与x的函数关系式是解题的关键,利用二次根式的性质进行化简是本题的难点.

练习册系列答案
相关题目
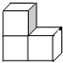 (2013•同安区一模)如图几何体的俯视图是( )
(2013•同安区一模)如图几何体的俯视图是( )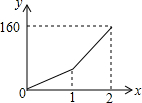 (2013•同安区一模)一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图所示,当0≤x≤1时,y关于x的函数解析式为y=60x;那么当1≤x≤2时,y关于x的函数解析式为( )
(2013•同安区一模)一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图所示,当0≤x≤1时,y关于x的函数解析式为y=60x;那么当1≤x≤2时,y关于x的函数解析式为( )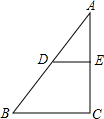 (2013•同安区一模)如图,已知:DE∥BC,∠ABC=40°,则∠ADE=
(2013•同安区一模)如图,已知:DE∥BC,∠ABC=40°,则∠ADE=