题目内容
【题目】已知,如图,AC⊥BC,HF⊥AB,CD⊥AB,∠1与∠2互补.求证:DE⊥AC. 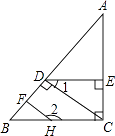
【答案】证明:如图所示,∵HF⊥AB,CD⊥AB, ∴CD∥HF,
∴∠2+∠3=180°,
又∵∠1与∠2互补,
∴∠2+∠1=180°,
∴∠1=∠3,
∴DE∥BC,
∵AC⊥BC,
∴DE⊥AC.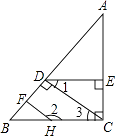
【解析】根据AC⊥BC,DE⊥AC,易证DE∥BC,那么∠2+∠3=180°,而∠1与∠2互补,从而可证∠1=∠3,即可得出DE∥BC,结合AC⊥BC,易得DE⊥AC.
【考点精析】通过灵活运用余角和补角的特征和平行线的判定与性质,掌握互余、互补是指两个角的数量关系,与两个角的位置无关;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质即可以解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某班学生分组做抛掷同一型号的一枚图钉的实验,大量重复实验的结果统计如下表:(顶尖朝上频率精确到 0.001)
累计实验次数 | 100 | 200 | 300 | 400 | 500 |
顶尖朝上次数 | 55 | 109 | 161 | 211 | 269 |
顶尖朝上频率 | 0.550 | 0.545 | 0.536 | 0.528 | 0.538 |
根据表格中的信息,估计掷一枚这样的图钉落地后顶尖朝上的概率为_______.