题目内容
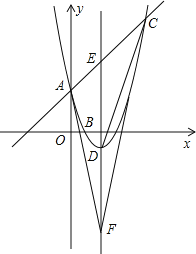
【题目】将一个矩形纸片
放置在平面直角坐标系中，点
点
点
是边
上的一点(点不与点
重合)，沿着
折叠该纸片，得点
的对应点
．
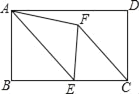
（1）如图①，当点落在边
上时，求点的坐标；
（2）若点落在边的上方，
与分别与边交于点
．
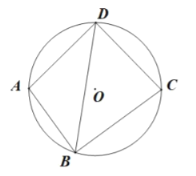
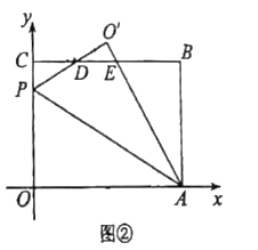
①如图②，当
时，求点
的坐标；
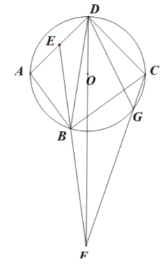
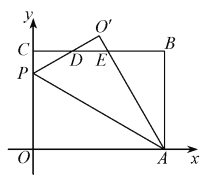
②当
时，求点的坐标(直接写出结果即可)．
【答案】（1）点
的坐标为
；（2）①
，②（
，6）．
【解析】
（1）根据矩形和折叠性质可知
，
，然后利用勾股定理求得
，从而求得
，由此确定点的坐标；
（2）①根据折叠的性质求得
，然后解直角三角形求得
，CD=
，从而确定D点坐标；
②根据角边角定理证得△CPD≌△
，从而求得
，然后设P（0，m），则
，
，
，
，利用勾股定理列方程求得m的值，从而求得
，设CD=x，则
，再用勾股定理列方程求x的值，从而求得D点坐标．
解：（1）∵点
，点
为矩形，
根据题意，由折叠可知
在
中，
点的坐标为
（2）①
，
，
，
∴在Rt△AOP中，
在Rt△CPD中，
，
∴CD=
∴D点坐标为（
，6）
②当
时，
∵
，
∴△CPD≌△
∴DE=DP
∴
设P（0，m），则，，
∴
∴在Rt△ABE中，
，解得：m=
∴
设CD=x，则
∴在Rt△CPD中，
，解得
∴D点坐标为（，6）．
练习册系列答案
中考解读考点精练系列答案
相关题目
【题目】某儿童游乐园推出两种门票收费方式：
方式一：购买会员卡，每张会员卡费用是
元，凭会员卡可免费进园
次，免费次数用完以后，每次进园凭会员卡只需
元；
方式二：不购买会员卡，每次进园是
元(两种方式每次进园均指单人)设进园次数为
( 为非负整数) ．
（1）根据题意，填写下表：
进园次数(次) |
|
|
| ··· |
方式一收费(元) |
|
| ··· | |
方式二收费(元) |
| ··· |
（2）设方式一收费
元，方式二收费
元，分别写出
的函数关系式;；
（3）当
时，哪种进园方式花费少?请说明理由．
