题目内容
 (2007•徐州)(A类)如图,已知AB是⊙O的直径,弦CD⊥AB于E,CD=16cm,AB=20cm,那么OE=
(2007•徐州)(A类)如图,已知AB是⊙O的直径,弦CD⊥AB于E,CD=16cm,AB=20cm,那么OE=6
6
cm.(B类)如图,已知AB是⊙O的直径,弦CD⊥AB于E,BE=4cm,CD=16cm,那么⊙O的半径是
10
10
cm.分析:A、连接OD,CD⊥AB,由垂径定理知,点E是CD的中点,CE=ED=8,直径AB=20,则半径OD=10,由勾股定理知,OE=6cm.
B、连接OD,CD⊥AB,由垂径定理知,点E是CD的中点,CE=ED=8,OE=OB-BE,在Rt△EDO中,由勾股定理知,
OE2+ED2=OD2即82+(OD-4)2=OD2,解得OD=10cm.
B、连接OD,CD⊥AB,由垂径定理知,点E是CD的中点,CE=ED=8,OE=OB-BE,在Rt△EDO中,由勾股定理知,
OE2+ED2=OD2即82+(OD-4)2=OD2,解得OD=10cm.
解答: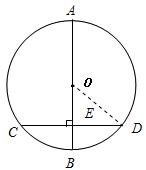 解:A、连接OD,
解:A、连接OD,
∵CD⊥AB,
∴点E是CD的中点,CE=ED=8,
∵AB=20,
∴OD=10,
在Rt△ODE中,OE2+ED2=OD2
解得,OE=6cm.
B、连接OD,
∵CD⊥AB,
∴点E是CD的中点,CE=ED=8,OE=OB-BE,
∴在Rt△EDO中,OE2+ED2=OD2即82+(OD-4)2=OD2,
解得OD=10cm.
 解:A、连接OD,
解:A、连接OD,∵CD⊥AB,
∴点E是CD的中点,CE=ED=8,
∵AB=20,
∴OD=10,
在Rt△ODE中,OE2+ED2=OD2
解得,OE=6cm.
B、连接OD,
∵CD⊥AB,
∴点E是CD的中点,CE=ED=8,OE=OB-BE,
∴在Rt△EDO中,OE2+ED2=OD2即82+(OD-4)2=OD2,
解得OD=10cm.
点评:本题利用了垂径定理,勾股定理求解.

练习册系列答案
相关题目