题目内容
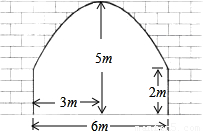
(2007•徐州)某隧道横断面由抛物线与矩形的三边组成,尺寸如图所示.(1)以隧道横断面抛物线的顶点为原点,以抛物线的对称轴为y轴,建立直角坐标系,求该抛物线对应的函数关系式;
(2)某卡车空车时能通过此隧道,现装载一集装箱箱宽3m,车与箱共高4.5m,此车能否通过隧道?并说明理由.
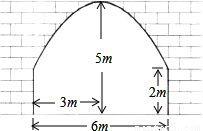
【答案】分析:(1)根据图中数据假设适当的解析式,用待定系数法求解;
(2)车从中间过,即x=1.5,代入解析式求出y值后,比较即可.
解答: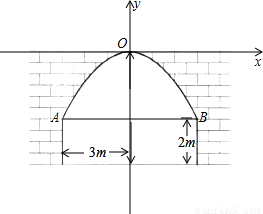 解:(1)设抛物线对应的函数关系式为y=ax2
解:(1)设抛物线对应的函数关系式为y=ax2
抛物线的顶点为原点,隧道宽6m,高5m,矩形的高为2m,
所以抛物线过点A(-3,-3),
代入得-3=9a,
解得a=- ,
,
所以函数关系式为y=-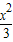 .
.
(2)如果此车能通过隧道,集装箱处于对称位置,
将x=1.5代入抛物线方程,得y=-0.75,
此时集装箱角离隧道的底为5-0.75=4.25米,不及车与箱总高4.5米,即4.25<4.5.
从而此车不能通过此隧道.
点评:求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.
(2)车从中间过,即x=1.5,代入解析式求出y值后,比较即可.
解答:
 解:(1)设抛物线对应的函数关系式为y=ax2
解:(1)设抛物线对应的函数关系式为y=ax2抛物线的顶点为原点,隧道宽6m,高5m,矩形的高为2m,
所以抛物线过点A(-3,-3),
代入得-3=9a,
解得a=-
 ,
,所以函数关系式为y=-
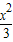 .
.(2)如果此车能通过隧道,集装箱处于对称位置,
将x=1.5代入抛物线方程,得y=-0.75,
此时集装箱角离隧道的底为5-0.75=4.25米,不及车与箱总高4.5米,即4.25<4.5.
从而此车不能通过此隧道.
点评:求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目